今回の理論記事は多層パーセプトロンと誤差逆伝播法による非線形なニューラルネットワーク学習について解説します。
多層パーセプトロン
前回記事で紹介した単純パーセプトロンは競馬などの線形非分離なデータを分離することができないという問題がありました。そこで、その問題を解決するために提案されたのが多層パーセプトロンです。多層パーセプトロンは以下の図のように、入力層と出力層の間に隠れ層がある構造をしています。
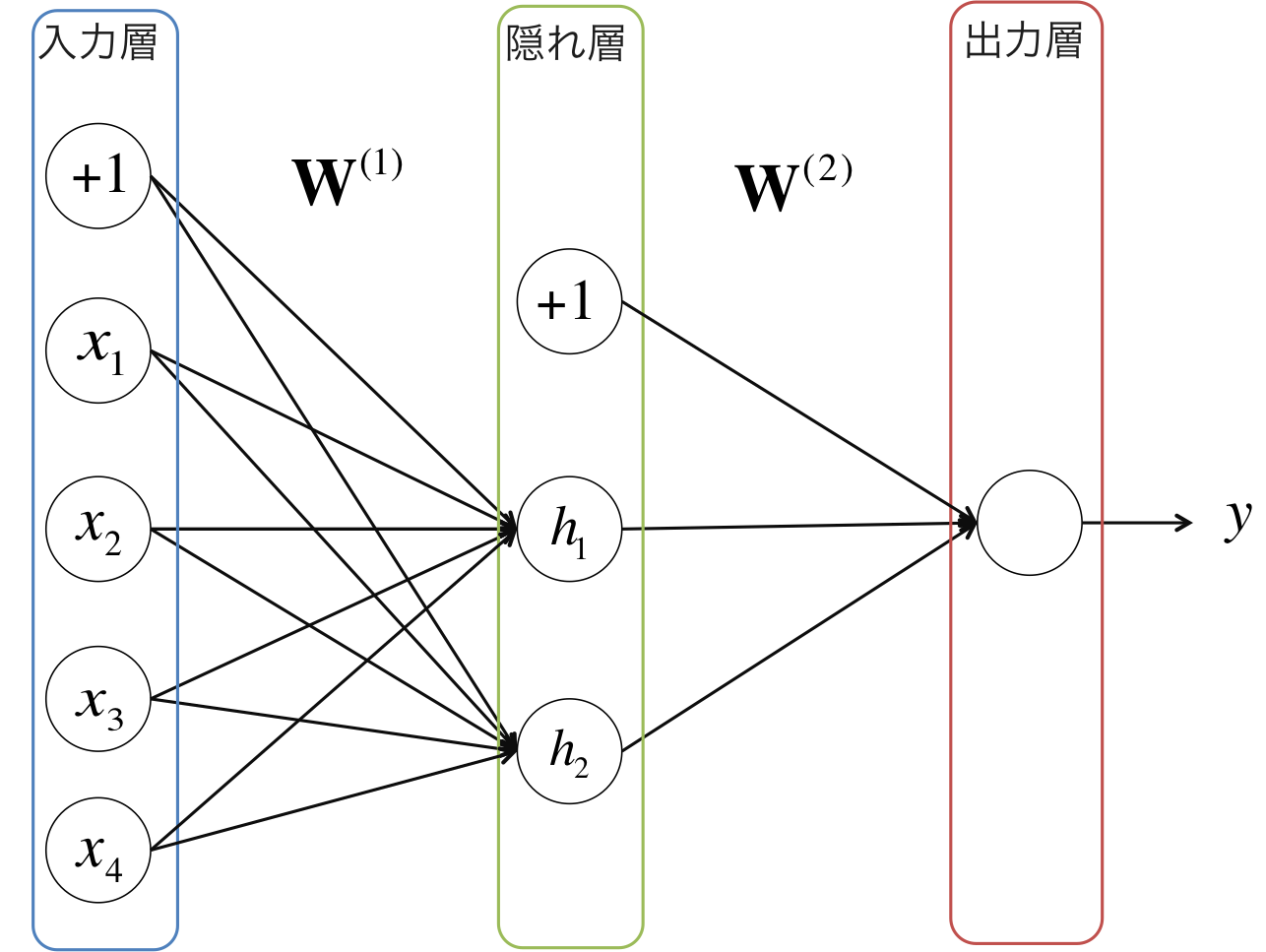
各層の間では、ユニット同士が重み付きのエッジ(辺)で結ばれており、その重みを行列 $ \mathbf{W}^{(l)} $ として表します。隠れ層のユニット $ h_j $ は $ \mathbf{x} $ の重み付き総和を入力として受け取り、微分可能な活性化関数 $ f $ によって非線形変換を行ないます。隠れユニット $ h_j $ の出力値は式(1)のように表されます。
$$ f(\sum_{j}w_j x_j) = f(\mathbf{w}^T \mathbf{x}) \tag{1}$$
活性化関数にはシグモイド関数、tanh、ReLUなど様々な関数が使われます。各活性化関数の形を比較した図を以下に示します。
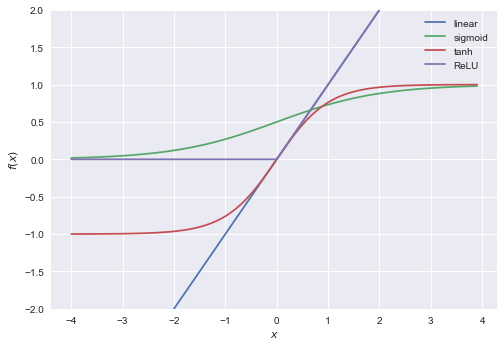
どの活性化関数を選ぶべきかは解く問題によって異なってきますが、ReLUはシグモイド関数やtanhに比べて計算コストが低く、多くのタスクにおいて高い精度が出ることが知られています。実際に以前AlphaImpactで使っていたニューラルネットワークのモデルには活性化関数としてReLUを採用していました。
出力層の活性化関数については、分類問題を解くのか、回帰問題を解くのかによって変わります。典型的には、二値分類問題のときはシグモイド関数、回帰問題のときは恒等写像を使うことが多いです。
また、重み $ \mathbf{W} $ の学習は、出力層から得られた $ y_n $ と教師ラベルである正解値 $ t_n $ との誤差を小さくするように更新をしていきます。誤差の指標となる損失関数は、 二値分類問題では式(2)で表される交差エントロピーが一般に用いられます。
$$ E_n = - t_n \log{y_n} - (1 - t_n) \log{(1 - y_n)} \tag{2}$$
一方、回帰問題では式(3)で表される二乗誤差が一般に用いられます。
$$ E_n = (t_n - y_n)^2 \tag{3}$$
いずれの損失関数にせよ、重み $ w^{(l)}_{kj} $ の更新量は、損失関数 $ E_n $ を偏微分し、訓練サンプルについて総和をとることにより式(4)のように求まります。
$$\Delta w^{(l)}_{kj} = - \eta \sum_n \frac{\partial E_n}{\partial w^{(l)}_{kj}} \tag{4}$$
しかし、多層パーセプトロンでは活性化関数が多重に掛かっているため、式(4)中の $ \partial E_n / \partial w_{ij}^{(l)} $ を求めるためには微分の連鎖規則を何度も適用する必要があり、多大な計算コストがかかってしまうという問題があります。そこで、次に説明する誤差逆伝播法(バックプロパゲーション)による学習規則を適用します。
誤差逆伝播法(バックプロパゲーション)
誤差逆伝播法のアルゴリズムによる重みパラメータの偏微分 $ \partial E_n / \partial w_{ij}^{(l)} $ の計算方法を解説します。
ステップ0: 準備
説明文中に出てくる変数の定義は以下の通りです:
| 変数名 | 意味 |
|---|---|
| $ L $ | レイヤー数 |
| $ \mathbf{x}_n $ | 訓練サンプル |
| $ \mathbf{t}_n $ | $ \mathbf{x}_n $ に対応する正解値 |
| $ \mathbf{y}_n $ | $ \mathbf{x}_n $ に対応する出力値 |
| $ E_n $ | $ \mathbf{x}_n $ に対応する誤差 |
| $ w_{ji}^{(l)} $ | 第 $ l $ 層 $ j $ 番目と第 $ l-1 $ 層 $ i $ 番目のユニット間の重み |
| $ u_j^{(l)} $ | 第 $ l $ 層 $ j $ 番目のユニットの入力 |
| $ z_j^{(l)} $ | 第 $ l $ 層 $ j $ 番目のユニットの出力 |
| $ f $ | 隠れ層の活性化関数 |
また、出力層の活性化関数は恒等写像または交差エントロピーを仮定します。
ステップ1: 順伝搬
入力層から訓練サンプル $ \mathbf{x}_n $ を入力し、出力層に向けて各層 $ l(=2,…,L) $ のユニットの入力 $ u_{j}^{(l)} $ (式(5))および出力 $ z_i^{(l)} $ (式(6))を計算します。
$$ u_j^{(l)}=\sum_{i} w_{ji}^{(l)} z_i^{(l-1)} \tag{5}$$
$$ z_i^{(l)}=f(u^{(l)}_i) \tag{6}$$

ステップ2: 逆伝播
式(7)により求められる出力層における $ \delta_j^{(L)} $ を計算します1。
$$\delta^{(L)}_j = y_j - t_j \tag{7}$$
次に、 $ \delta^{(L)}_j $ を起点として、隠れ層 $ l $ における $ \delta^{(l)}_j(l=L-1,L-2,…,2) $ を式(8)により再帰的に計算します。
$$\delta_j^{(l)} = \sum_k \delta_k^{(l+1)} w_{kj}^{(l+1)}f’(u_j^{(l)}) \tag{8}$$
ここで重要なのは、第 $ l+1 $ 層の $ \delta_k^{(l+1)} $ の計算結果から、第 $ l $ 層の $ \delta_j^{(l)} $ がドミノ式に計算できるということです。このとき、 $ \delta_j $ が入力→出力の向きに対して逆向きに伝播するため、このアルゴリズムを誤差逆伝播法と呼びます。
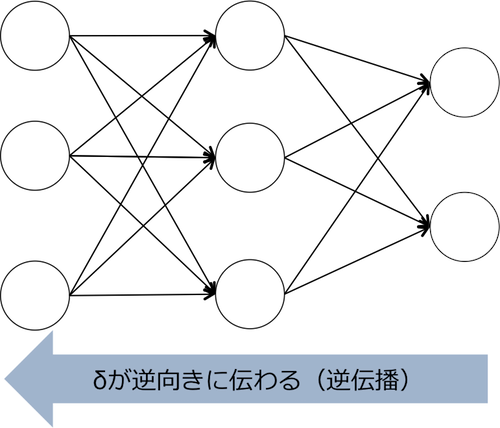
ステップ3: $ w_{ji}^{(l)} $ の偏微分を計算する
各層 $ l $ の重みパラメータ $ w_{ji}^{(l)} $ について、ステップ1、2で求めた $ z_i^{(l-1)} $ および $ \delta_j^{(l)} $ を式(9)に代入し、目的の微分が求められます。
$$\frac{\partial E_n}{\partial w_{ji}^{(l)}} = \delta_j^{(l)} z_i^{(l-1)} \tag{9}$$
『距離適性』で多層パーセプトロンを直感的に理解する
ここまでの解説はややこしい計算式が多くて難解でしたが、多層にすると何が嬉しいのか?ということをもう少し直感的に理解できるように解説したいと思います。
まず、競走馬の長距離適性 or 短距離適性とコースの長距離 or 短距離の変数が与えられているとします。それらの変数から以下の図のように『強い』『弱い』を分類するという問題を考えてみましょう。
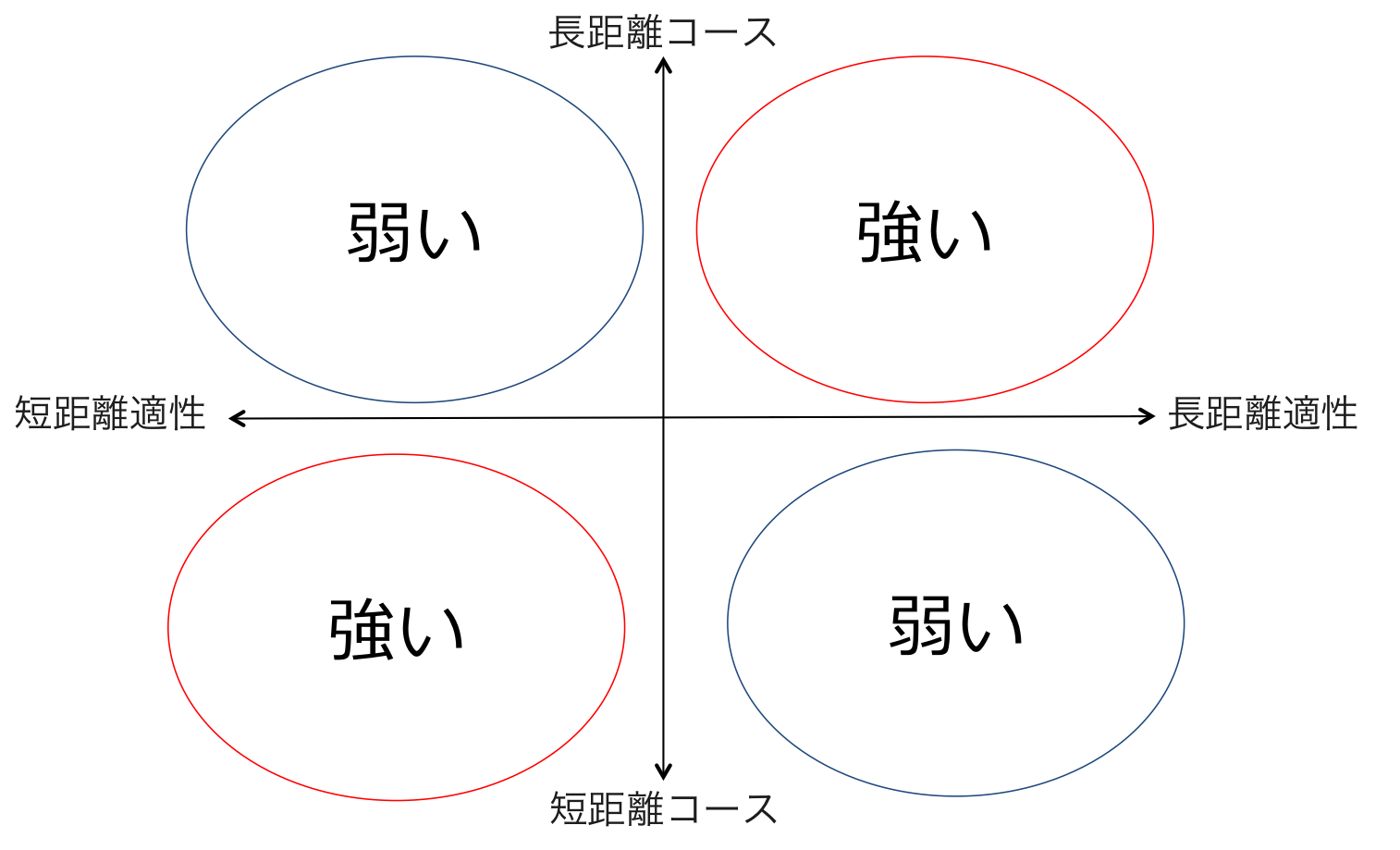
上図のような排他的論理和(XOR)の関係は直線で分離することができないので、線形非分離な単純パーセプトロンなどの識別器では正しく分類することができません。そこで、上図の距離適性とコース距離の関係を隠れ層1層の多層パーセプトロンに学習させると、以下のようなネットワークが得られます。

上図において、エッジの太さは対応する重みパラメータの大きさを表しています。隠れ層の部分に注目すると、上のユニットは長距離適性と長距離コース、下のユニットは短距離適性と短距離コースと強く結合していることがわかります。この多層パーセプトロンに『長距離コースを走る長距離適性馬』を表す入力を与えると、以下の図のように上の隠れユニットが活性化し、その信号が出力層に伝わって「強」という結果が出力されます。
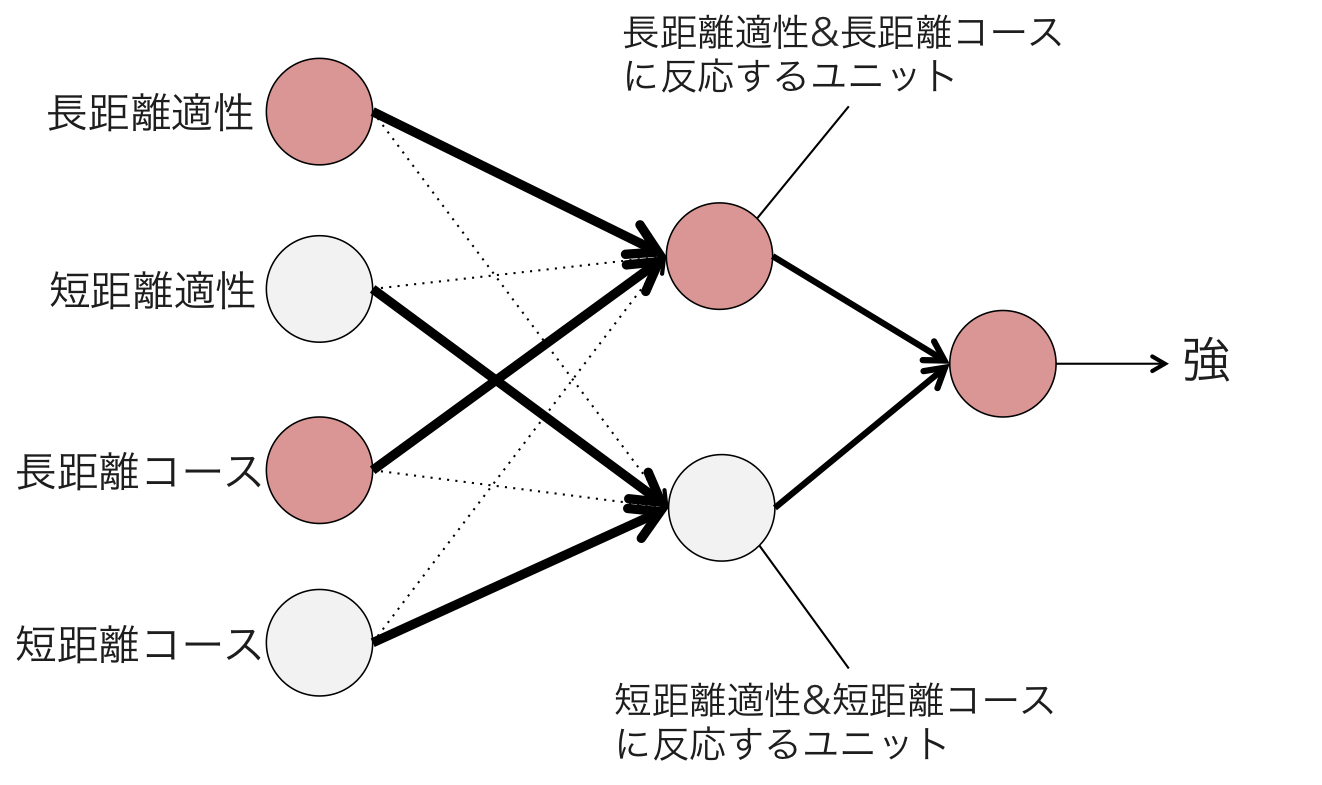
一方、『短距離コースの長距離適性馬』を表す入力を与えると、入力の信号は2つの隠れユニットに分散して伝わります。その結果、どちらの隠れユニットも活性化できるほど十分強い信号が受けとれないため、出力層に信号が届かず「弱」という結果が出力されます。
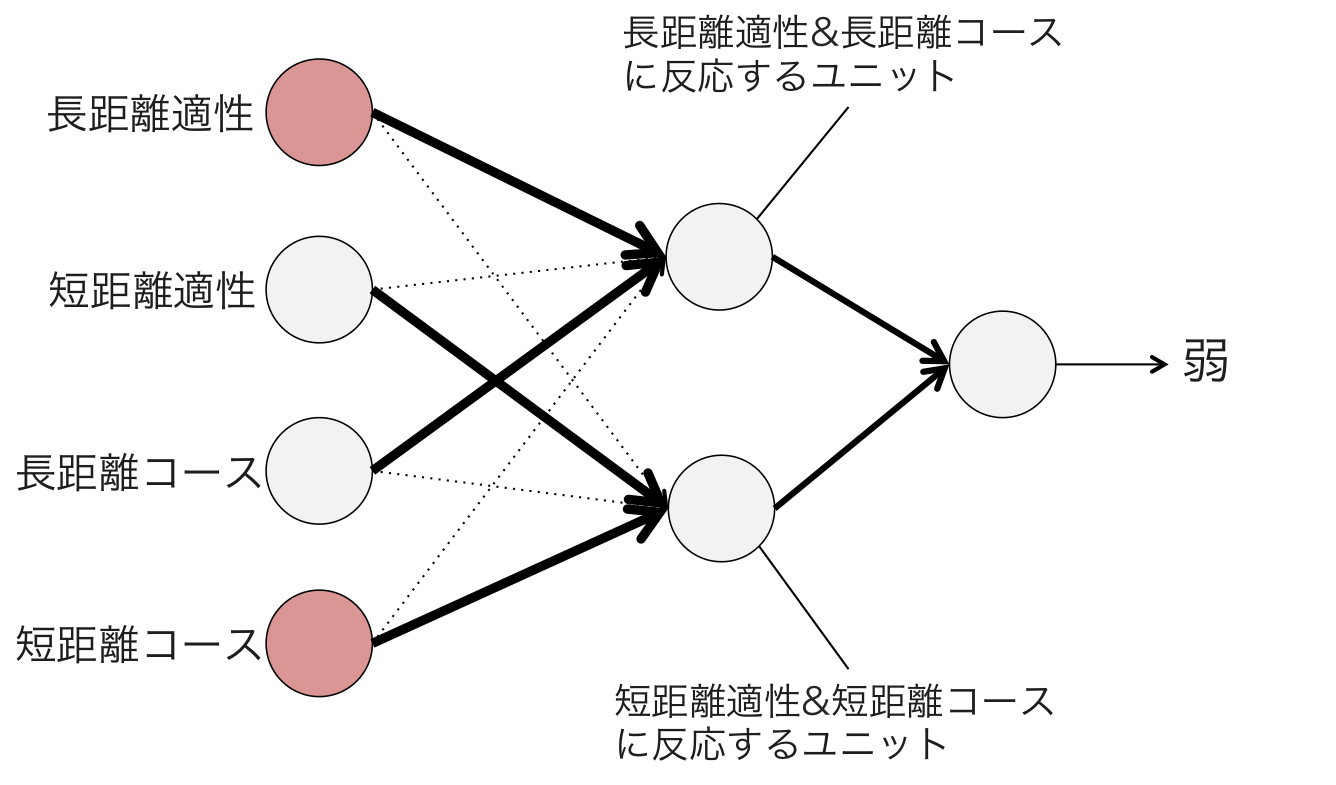
同様にして、『短距離コースの長距離適性馬』は「弱」、『短距離コースの短距離適性場』は「強」という出力が得られるので、目的とした「距離敵性とコース距離」の分類ができたということになります。この例のように、パーセプトロンの層を多層にすることによって、単純パーセプトロンでは表現できなかった非線形なパターンを分類できるようになるのです。また、多層パーセプトロンは層の数とユニットの数を無制限に増やすことによって、任意の連続関数について近似可能であるということが理論的に証明されています2。
実験設定
実験設定はこれまでの記事と同様に東京芝2,400mの古馬戦の条件で、分類問題は複勝圏内に入るかどうかの2クラス分類、回帰問題は走破タイム回帰を解きます。
特徴量も過去の実験と同様に、以下の14個を用います。
| 特徴量名 | カラム名 | 説明 |
|---|---|---|
| 出走頭数 | num_horse | レースに出走する頭数 |
| 1着賞金 | win_prize | レースレベルの指標 |
| 馬齢 | age | 馬の年齢 |
| 性別 | gender | 牡・牝のダミー変数(騙馬は少ないのでダミー変数にしない) |
| 斤量 | burden | kg |
| 脚質 | run_style | 逃げ=1, 先行=2, 差し=3, 追込=4 |
| 馬複勝率 | place_ratio | 馬の通算複勝率 |
| 前走距離 | prev_length | メートル |
| 前走タイム差 | prev_time_diff | 1着との秒差 |
| 前走前3Fタイム | prev_first3f | 秒 |
| 前走後3Fタイム | prev_last3f | 秒 |
| 馬体重 | horse_weight | kg |
| 馬体重増減 | delta_weight | kg |
| 騎手複勝率 | jockey_place_ratio | 過去1ヶ月の騎手の複勝率 |
各特徴量はスケールが大きく異なると上手く学習ができない原因となるので、平均0、分散1になるように標準化処理をします。また、多層パーセプトロンの実装には、scikit-learnのMLPClassifierおよびMLPRegressorを利用しました。
パラメータについては以下のように設定しました。
| パラメータの種類 | 値 |
|---|---|
| 隠れ層の数 | 1層 |
| 隠れユニット数 | 1~14 |
| 活性化関数 | ReLU |
| 最適化アルゴリズム | SGD |
| バッチサイズ | 128 |
| alpha (L2正則化パラメータ) | 0.0001(デフォルト値) |
| 学習係数 | $ 1^0 $ 〜 $ 1^{-6}$$ |
| 最大更新回数 | 5000 |
隠れユニット数と学習係数はグリッドサーチで誤差関数が最小となるパラメータを選択しました。また、二値分類では正例と負例のサンプル数のバランスをとるため、サンプル数が等しくなるようにネガティブサンプリングをしました。
ベースラインの評価
評価のベースラインとして、今回も過去記事と同様に単勝人気順位のTop-N Boxの評価を使います。評価値は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.314 0.717 1.132
place 0.629 0.786 0.616
---- Top-2 BOX
hit ret ret_std
win 0.486 0.680 0.787
place 0.800 0.766 0.466
quinella place 0.314 0.697 1.085
quinella 0.143 0.457 1.168
exacta 0.143 0.527 1.448
---- Top-3 BOX
hit ret ret_std
win 0.543 0.536 0.561
place 0.914 0.754 0.331
quinella place 0.543 0.634 0.765
quinella 0.200 0.250 0.529
exacta 0.200 0.245 0.539
trio 0.086 0.466 1.690
trifecta 0.086 0.253 0.918
---- Top-4 BOX
hit ret ret_std
win 0.686 0.669 0.642
place 0.971 0.746 0.254
quinella place 0.743 0.638 0.609
quinella 0.343 0.405 0.696
exacta 0.343 0.381 0.670
trio 0.171 0.416 1.032
trifecta 0.171 0.292 0.773
---- Top-5 BOX
hit ret ret_std
win 0.800 0.765 0.668
place 0.971 0.741 0.269
quinella place 0.886 0.710 0.642
quinella 0.514 0.608 0.831
exacta 0.514 0.595 0.878
trio 0.314 0.507 1.064
trifecta 0.314 0.513 1.331
複勝圏内確率の予測
Top-N Box 評価
多層パーセプトロンによる複勝圏内分類のTop-N Box評価は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.235 0.512 0.987
place 0.647 1.344 2.874
---- Top-2 BOX
hit ret ret_std
win 0.294 0.346 0.578
place 0.706 1.085 1.519
quinella place 0.353 1.644 2.945
quinella 0.118 1.612 5.654
exacta 0.118 1.119 3.910
---- Top-3 BOX
hit ret ret_std
win 0.441 0.525 0.761
place 0.941 1.059 0.952
quinella place 0.500 0.910 1.183
quinella 0.235 0.846 2.067
exacta 0.235 0.673 1.583
trio 0.088 0.676 2.745
trifecta 0.088 0.566 2.568
---- Top-4 BOX
hit ret ret_std
win 0.529 0.626 1.033
place 0.971 0.879 0.722
quinella place 0.559 0.678 0.998
quinella 0.353 0.739 1.441
exacta 0.353 0.704 1.582
trio 0.147 0.600 2.053
trifecta 0.147 0.678 2.774
---- Top-5 BOX
hit ret ret_std
win 0.588 0.613 0.905
place 1.000 0.774 0.547
quinella place 0.676 0.486 0.608
quinella 0.471 0.592 0.921
exacta 0.471 0.584 1.024
trio 0.176 0.296 0.867
trifecta 0.176 0.339 1.161
単勝的中率はそこまで高くないですが、複勝の的中精度はランダムフォレストやSVMよりも優れており、さらにこれまでの実験で越えられなかったベースライン(人気順)の精度をも上回りました。解いている問題が複勝予測であるので、単勝よりも複勝の精度が高いというのは理にかなった結果だと言えるでしょう。さらに的中率が高いだけでなく、Top-1の回収率も134%と非常に高い評価値となっており、東京芝2,400m古馬戦ではとてつもない強さを発揮することが期待されます。
走破タイム予測
多層パーセプトロンの走破タイム予測のTop-N Box評価は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.294 1.456 4.221
place 0.412 0.676 1.051
---- Top-2 BOX
hit ret ret_std
win 0.412 1.074 2.264
place 0.588 0.691 0.706
quinella place 0.206 0.694 1.753
quinella 0.088 1.015 4.431
exacta 0.088 0.812 3.452
---- Top-3 BOX
hit ret ret_std
win 0.559 0.946 1.594
place 0.794 0.625 0.427
quinella place 0.294 0.317 0.625
quinella 0.118 0.363 1.478
exacta 0.118 0.299 1.156
trio 0.000 0.000 0.000
trifecta 0.000 0.000 0.000
---- Top-4 BOX
hit ret ret_std
win 0.559 0.710 1.195
place 0.882 0.626 0.364
quinella place 0.412 0.457 0.697
quinella 0.324 0.509 1.054
exacta 0.324 0.391 0.779
trio 0.176 0.459 1.090
trifecta 0.176 0.328 0.849
---- Top-5 BOX
hit ret ret_std
win 0.588 0.656 1.036
place 0.912 0.615 0.365
quinella place 0.559 0.470 0.564
quinella 0.324 0.306 0.632
exacta 0.324 0.235 0.468
trio 0.206 0.261 0.600
trifecta 0.206 0.209 0.545
走破タイム予測は、複勝予測とは異なり、複勝よりも単勝の性能が高い傾向が見られます。複勝予測では1着の馬と3着の馬は同じ扱いですが、走破タイム予測ではタイムが目的変数であるため1着≧3着ということを学習しています。その違いが単勝特化と複勝特化の傾向の差として現れているのだと考えられます。また、単勝的中精度に限ればランダムフォレストやSVMの実験結果と比較して最も高い評価値となっており、非常に高い予測性能があるということがわかります。
2016年ジャパンカップを予測する
最後に恒例の2016年ジャパンカップの複勝確率と走破タイムの予測結果を紹介します。
まず、レース結果は以下の通りです。
| 着順 | 馬番 | 馬名 | 人気 | 走破タイム |
|---|---|---|---|---|
| 1 | 1 | キタサンブラック | 1 | 2:25.8 |
| 2 | 12 | サウンズオブアース | 5 | 2:26.2 |
| 3 | 17 | シュヴァルグラン | 6 | 2:26.3 |
| 4 | 3 | ゴールドアクター | 3 | 2:26.4 |
| 5 | 16 | リアルスティール | 2 | 2:26.4 |
| 6 | 14 | レインボーライン | 8 | 2:26.4 |
| 7 | 5 | イキートス | 16 | 2:26.4 |
| 8 | 7 | ワンアンドオンリー | 14 | 2:26.6 |
| 9 | 4 | ルージュバック | 7 | 2:26.8 |
| 10 | 6 | ラストインパクト | 13 | 2:26.9 |
| 11 | 10 | トーセンバジル | 12 | 2:26.9 |
| 12 | 15 | ナイトフラワー | 9 | 2:26.9 |
| 13 | 9 | ディーマジェスティ | 4 | 2:27.1 |
| 14 | 8 | イラプト | 10 | 2:27.1 |
| 15 | 13 | ヒットザターゲット | 17 | 2:27.2 |
| 16 | 2 | ビッシュ | 11 | 2:27.2 |
| 17 | 11 | フェイムゲーム | 15 | 2:27.3 |
次に多層パーセプトロンによる予測結果です。
▼ 複勝圏内予測
| 予測順位 | 馬番 | 馬名 | 予測複勝確率 |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 0.649 |
| 2 | 12 | サウンズオブアース | 0.558 |
| 3 | 14 | レインボーライン | 0.525 |
| 4 | 2 | ビッシュ | 0.472 |
| 5 | 16 | リアルスティール | 0.453 |
| 6 | 4 | ルージュバック | 0.432 |
| 7 | 9 | ディーマジェスティ | 0.404 |
| 8 | 6 | ラストインパクト | 0.318 |
| 9 | 10 | トーセンバジル | 0.292 |
| 10 | 3 | ゴールドアクター | 0.290 |
| 11 | 17 | シュヴァルグラン | 0.222 |
| 12 | 15 | ナイトフラワー | 0.175 |
| 13 | 8 | イラプト | 0.151 |
| 14 | 7 | ワンアンドオンリー | 0.117 |
| 15 | 5 | イキートス | 0.077 |
| 16 | 13 | ヒットザターゲット | 0.028 |
| 17 | 11 | フェイムゲーム | 0.024 |
▼ 走破タイム予測
| 予測順位 | 馬番 | 馬名 | 予測タイム |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 2:23.34 |
| 2 | 12 | サウンズオブアース | 2:23.89 |
| 3 | 16 | リアルスティール | 2:23.91 |
| 4 | 10 | トーセンバジル | 2:23.94 |
| 5 | 9 | ディーマジェスティ | 2:23.99 |
| 6 | 17 | シュヴァルグラン | 2:24.10 |
| 7 | 6 | ラストインパクト | 2:24.37 |
| 8 | 2 | ビッシュ | 2:24.39 |
| 9 | 14 | レインボーライン | 2:24.44 |
| 10 | 7 | ワンアンドオンリー | 2:24.51 |
| 11 | 3 | ゴールドアクター | 2:24.55 |
| 12 | 4 | ルージュバック | 2:25.13 |
| 13 | 11 | フェイムゲーム | 2:25.26 |
| 14 | 13 | ヒットザターゲット | 2:25.27 |
| 15 | 15 | ナイトフラワー | 2:25.69 |
| 16 | 5 | イキートス | 2:25.91 |
| 17 | 8 | イラプト | 2:26.24 |
複勝圏内予測も走破タイム予測も見事にキタサンブラック→サウンズオブアースの1,2着を的中させています。1,2着を上位2頭でピッタリ的中させられたモデルは過去の実験にはなかったので、定量評価が示していた通り、これまで試してきたモデルと比べても高い予測性能を持っていると考えられます。
おわりに
今回は多層パーセプトロンと誤差逆伝播法のアルゴリズムを紹介しました。誤差逆伝播法の説明は数式が多く、途中で読むのを諦めてしまった方もいらっしゃるかもしれませんが、今はTheanoやTensorFlowといった数理計算ライブラリが充実しており、動かすだけならコマンド1つで自動微分できてしまう時代なので、あまり心配することはありません。とは言え、裏側の理論を理解していると、モデルのパラメータチューニングなどで必要となる職人の勘が磨かれるので、知っておいて損はないでしょう。
多層パーセプトロンによる予測実験では、これまで試してきたモデルの中で最も良い評価結果が得られました。正直、たった14個のありきたりな特徴量でこれほど高い精度が出るとは思っていなかったので、自分でも驚いてしまいました。ニューラルネットワークのポテンシャルの高さは計り知れません。
次回も競馬で学ぶニューラルネットワークシリーズを書く予定です。お楽しみに。
-
出力層の活性化関数が恒等写像または交差エントロピーの場合、式(8)を計算すると式(7)が導出されます。 ↩︎
-
この定理はUniversal approximation theoremと呼ばれます。 ↩︎