今回の記事ではディープラーニングの説明に入る前に、ニューラルネットワークの基本形であるパーセプトロンについて説明していきます。
パーセプトロン
我々生物の脳は無数の神経細胞(ニューロン)から構成されており、その神経細胞の相互的な電気信号によって学習や思考といった機能を獲得しています。人工知能の分野において、ニューロンの神経ネットワークを模倣した計算モデルをニューラルネットワークと呼びます。
ニューラルネットワークの研究は約半世紀以上も前から行われており、長い歴史があります。1958年にフランク・ローゼンブラットが提案したパーセプトロンは現在広く使われているニューラルネットワークやディープラーニングの基礎となっている理論です。パーセプトロンは $ y={+1, -1} $ を識別する二値分類器であり、以下の図ようにS層、A層、R層の3層から構成されています。

S層(入力層)に入力された信号はA層(中間層)で重み係数 $ w_j $ が掛けられ、その総和 $ z $ が出力層のユニットに入力されます。総和 $ z $ は以下の式のように表されます。
$$ z = \sum_{j}w_j x_j \tag{1}$$
そして、出力層のユニットでは信号の総和 $ z $ があるしきい値 $ \theta $ 以上だったときに $ +1 $ 、 $ \theta $ 未満のときに $ -1 $ となるような変換を行ないます。この変換には以下で表されるヘビサイド関数が用いられます。
$$\begin{eqnarray}f(z) =\begin{cases}1 & (z \geqq \theta) \\\-1 & (z < \theta)\end{cases} \tag{2}\end{eqnarray}$$
一般には、 $ w_0=\theta $ 、 $ x_0=+1 $ と置いて、 $ z=\sum_{j}w_j x_j=\mathbf{w}^T\mathbf{x} $ として簡潔に表現します。
このような一定以上の強い信号が来た時にユニットがアクティブになる挙動は、脳のニューロンが一定以上の電気信号を受け取ると発火し、シナプスで結合している別のニューロンに神経伝達物質が伝わる機能をモデル化したものです。ユニットが発火するかどうかを決定する関数は活性化関数と呼ばれ、ヘビサイド関数はその中で最も単純な関数の1つです。活性化関数には非連続な関数の他に、シグモイド関数やtanhなどの微分可能な関数もあり、現在ではそちらが主流になっています。また、中間層が1層の単純パーセプトロンの活性化関数にシグモイド関数を選ぶと、第8回理論記事で紹介したロジスティック回帰と等価な識別器になることが知られています。
パーセプトロンの学習規則は以下のステップにより行われます:
- 重みベクトル $ \mathbf{w} $ を適当に初期化する
- 入力 $ \mathbf{x_i} $ に対する予測ラベルを $ \hat{y_i} $ 、正解ラベルを $ y_i $ としたとき、以下の式により重み係数を更新する$$\mathbf{w} \leftarrow \mathbf{w} + \eta (y_i - \hat{y_i}) \mathbf{x_i} \tag{3}$$
- 収束するか、最大更新回数(最大エポック数)に達するまでステップ2を繰り返す
ただし、式(3)中の $ \eta $ は正の値をとる学習係数です。パーセプトロンの学習規則による重みの更新は、訓練サンプルのクラスラベル $ {+1, -1} $ が線形分離可能な場合にのみ収束することが証明されています。そのため、競馬予測のように線形非分離不可能なデータに対して学習を行なうときは、最大更新回数(最大エポック数)を設定しないと無限に更新が続いてしまうので注意が必要です。
実験設定
今回の実験には中間層が1層で、出力層の活性化関数をヘビサイド関数とした古典的な単純パーセプトロンを用います。解く問題は過去記事の分類問題の設定と同様に、複勝圏内に入るかどうかの2クラス分類とします。
特徴量はこれまでの実験と同様に以下の14個を用います。
| 特徴量名 | カラム名 | 説明 |
|---|---|---|
| 出走頭数 | num_horse | レースに出走する頭数 |
| 1着賞金 | win_prize | レースレベルの指標 |
| 馬齢 | age | 馬の年齢 |
| 性別 | gender | 牡・牝のダミー変数(騙馬は少ないのでダミー変数にしない) |
| 斤量 | burden | kg |
| 脚質 | run_style | 逃げ=1, 先行=2, 差し=3, 追込=4 |
| 馬複勝率 | place_ratio | 馬の通算複勝率 |
| 前走距離 | prev_length | メートル |
| 前走タイム差 | prev_time_diff | 1着との秒差 |
| 前走前3Fタイム | prev_first3f | 秒 |
| 前走後3Fタイム | prev_last3f | 秒 |
| 馬体重 | horse_weight | kg |
| 馬体重増減 | delta_weight | kg |
| 騎手複勝率 | jockey_place_ratio | 過去1ヶ月の騎手の複勝率 |
また、パーセプトロンの実装にはscikit-learnのPerceptronを利用しました。
重み係数の更新回数の上限は1000回として、その他のパラメータはデフォルト値としました。また、特徴量間のスケールを統一するために、前処理として標準化を行ないました。
学習の進行
更新ステップごとの精度の変化をグラフに示します。精度の指標には正規化相互情報量(NMI)を用いました。
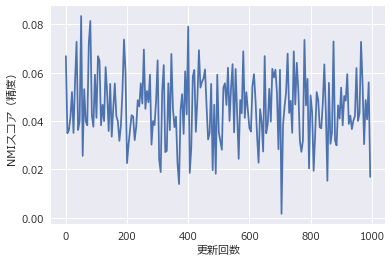
学習がどれだけ進行しても収束しそうにないことがわかります。これは競馬のデータが線形非分離であるためで、妥当な結果と言えるでしょう。
予測ラベルを可視化する
1000回の更新の中で最もNMIスコアが高かったときの重み係数で評価用テストデータの予測をしたときの結果を可視化してみます。高次元データの可視化は、多次元尺度法であるt-SNE1を利用して2次元平面上へ射影した点をプロットします。
まずは、正解ラベルを可視化した結果です。
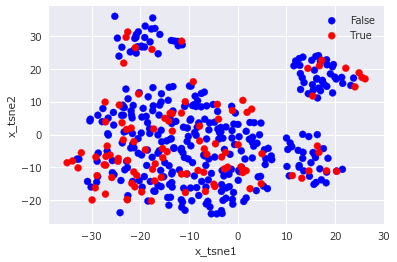
次に、単純パーセプトロンによる予測ラベルを可視化した結果です。
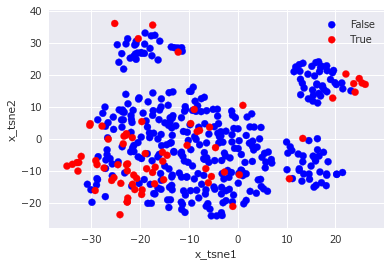
図中のx_tsne1とx_tsne2はt-SNEにより15次元の入力データを2次元に圧縮した後の値を示しています。
正解ラベルと予測ラベルを見比べてみると、左下と右上のTrueラベルをいくつか的中させているので、多少の予測性能は有していると推測されます。
2016年ジャパンカップを予測する
レース結果と単純パーセプトロンによる予測ラベルは以下の通りです。
| 着順 | 馬番 | 馬名 | 人気 | 予測ラベル(複勝圏内) |
|---|---|---|---|---|
| 1 | 1 | キタサンブラック | 1 | False |
| 2 | 12 | サウンズオブアース | 5 | False |
| 3 | 17 | シュヴァルグラン | 6 | False |
| 4 | 3 | ゴールドアクター | 3 | False |
| 5 | 16 | リアルスティール | 2 | False |
| 6 | 14 | レインボーライン | 8 | True |
| 7 | 5 | イキートス | 16 | False |
| 8 | 7 | ワンアンドオンリー | 14 | False |
| 9 | 4 | ルージュバック | 7 | False |
| 10 | 6 | ラストインパクト | 13 | False |
| 11 | 10 | トーセンバジル | 12 | False |
| 12 | 15 | ナイトフラワー | 9 | False |
| 13 | 9 | ディーマジェスティ | 4 | True |
| 14 | 8 | イラプト | 10 | False |
| 15 | 13 | ヒットザターゲット | 17 | False |
| 16 | 2 | ビッシュ | 11 | False |
| 17 | 11 | フェイムゲーム | 15 | False |
レインボーラインとディーマジェスティの2頭が複勝圏内に入るという予測結果となりました。中穴狙いの渋い予想ですが、これまでの実験で試したSVMやランダムフォレストなどはキタサンブラックを最上位に予測できていたことを考えると、単純パーセプトロンはあまり精度が高くないということが見てとれます。
まとめ
今回はニューラルネットワークの中でも最もシンプルな単純パーセプトロンによる競馬予測を試しました。単純パーセプトロンは理解が容易く、機械学習の導入には良い手法ですが、非線形なデータだと収束しないという性質は競馬を含む多くの実問題に適用するときの障害となります。そういうわけで、次回はその問題を解決するため、誤差逆伝播法(バックプロパゲーション)で学習を行なう多層ニューラルネットワークを使って競馬予測をしていきたいと思います。