第10回の理論記事では決定木とランダムフォレストを使った競馬予測をしていきます。
決定木
決定木とは木構造をした決定を行なうグラフにより、分類や回帰を行なう教師あり学習アルゴリズムです。決定木はSVMなどと異なり出力に至る過程を木構造として視覚的に捉えることができるという点で優れています。
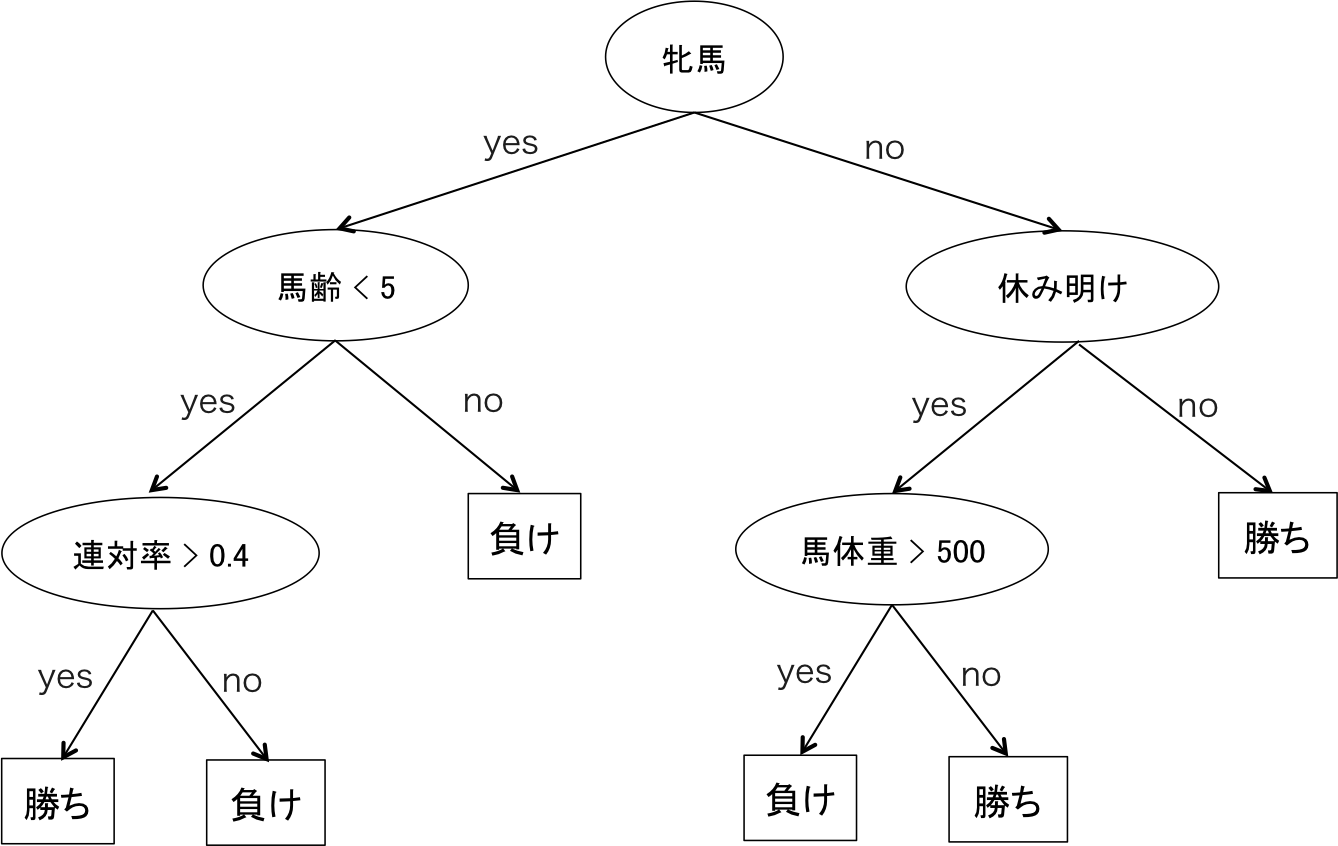
決定木の生成のゴールは、オッカムの剃刀1の原則に従い、なるべく少ない識別規則でクラスの識別を行なうことです。分岐に使う特徴量の決定は、分割することによる情報利得が最大となるものを選択します。情報利得の指標にはジニ係数やエントロピーを使うのが一般的です。また、木の構造をなるべく単純にするために識別規則を削除していく操作を剪定といいます。
決定木の生成アルゴリズムはCARTやC4.5が代表的です。決定木はCARTのようにデータを2分割していく2分木と、C4.5のように多分木構造を許すものがあります。
決定木は、欠損値を欠損値として扱うこができる、特徴量のスケールの違いに影響を受けず、標準化のような前処理をしなくても良いというメリットがあり、競馬を含め現実的な問題に適しています。一方、識別規則が単純なため分散が大きく、入力データの違いによる影響を受けやすいという問題があります。そのような欠点を解消したアルゴリズムが、次に説明するランダムフォレストです。
ランダムフォレストとは?
ランダムフォレストは、入力となる学習データと識別ルールに使う特徴量をランダム選択し、多数の決定木を作成して多数決を取るアルゴリズムです。一般に、複数の弱識別器を組合せることで強識別器を構成する学習方法を集団学習(アンサンブル学習)と呼びます。ランダムフォレストもアンサンブル学習の1つです。ランダムフォレストの概要図は以下の通りです。
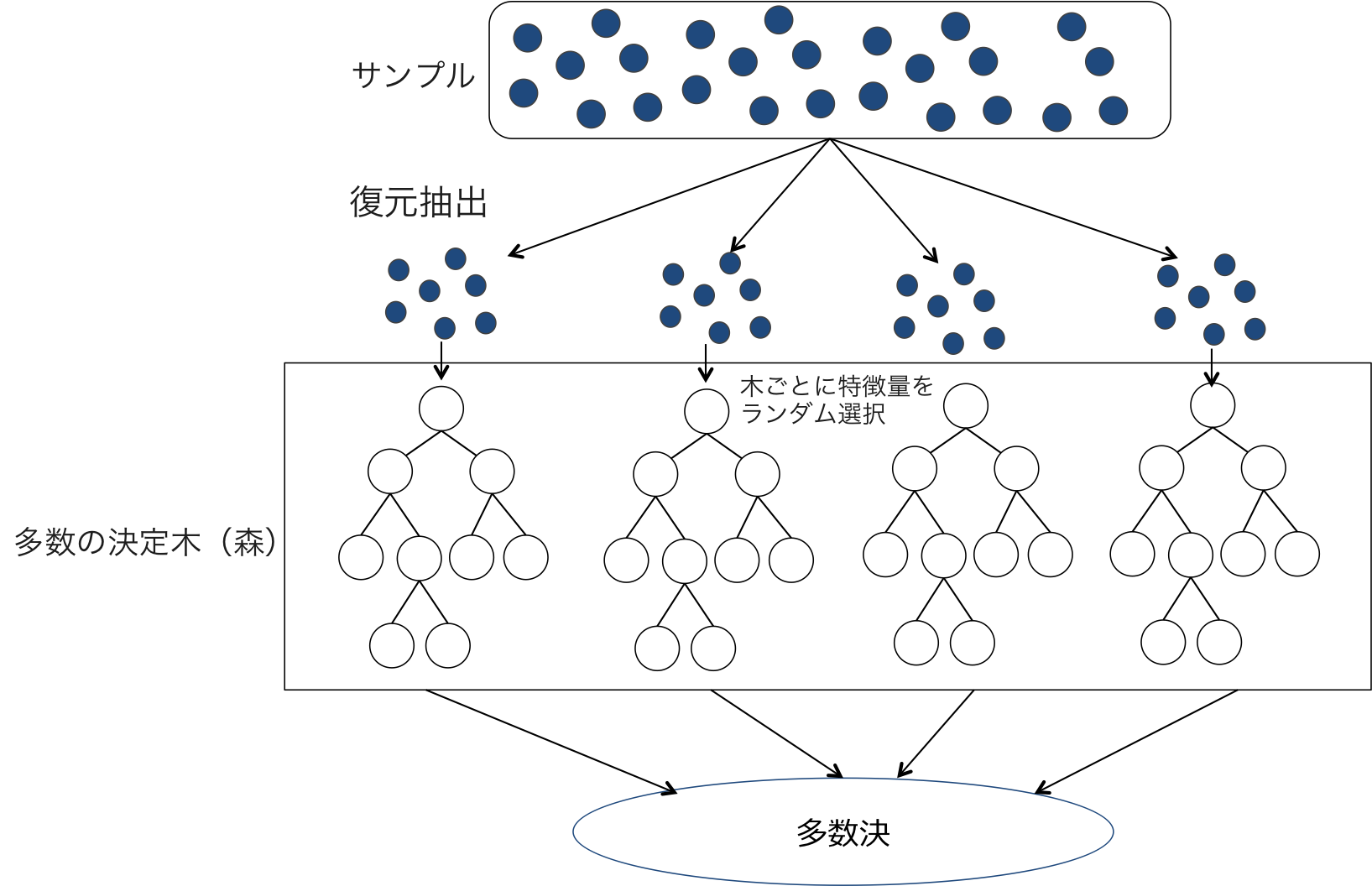
ランダムフォレストに限らず、学習データを繰り返しを許す復元抽出でサンプリングし、出力結果の多数決をとるアンサンブル学習の方法をバギングと呼びます。バギングをすることで、各識別器は異なるデータで学習を行なうことになるため、データの偏りの影響を受けにくくなります。さらに、ランダムフォレストはそのバギングに加えて、決定木ごとに識別で使う特徴量もランダムに選択しています。このように入力データと使う特徴量をランダムにすることで、決定木同士の相関を減らすことができます。これを競馬に例えれば、ある人は血統で予想して、またある人はスピード指数で予想して、最後にその予想家たちの意見を多数決するということになります。
ランダムフォレストは決定木ベースのアルゴリズムなのでデータのスケールに影響を受けないという強みがあるだけでなく、特徴量ごとの重要度を測ることができるため、機械学習アルゴリズムの中でも特に人気が高いです。また、決定木の種類として分類木だけでなく回帰木も使えるため、回帰モデルとして使うこともできます。
実験設定
実験設定は前回の記事と同様に東京芝2,400mの古馬戦の条件で、分類問題は複勝圏内に入るかどうかの2クラス分類、回帰問題は走破タイム回帰を解きます。使うモデルは複勝予測では分類木を使った決定木とランダムフォレスト、走破タイム予測では回帰木を使った決定木とランダムフォレストです。
特徴量も前回と同様に、以下の14個を用います。
| 特徴量名 | カラム名 | 説明 |
|---|---|---|
| 出走頭数 | num_horse | レースに出走する頭数 |
| 1着賞金 | win_prize | レースレベルの指標 |
| 馬齢 | age | 馬の年齢 |
| 性別 | gender | 牡・牝のダミー変数(騙馬は少ないのでダミー変数にしない) |
| 斤量 | burden | kg |
| 脚質 | run_style | 逃げ=1, 先行=2, 差し=3, 追込=4 |
| 馬複勝率 | place_ratio | 馬の通算複勝率 |
| 前走距離 | prev_length | メートル |
| 前走タイム差 | prev_time_diff | 1着との秒差 |
| 前走前3Fタイム | prev_first3f | 秒 |
| 前走後3Fタイム | prev_last3f | 秒 |
| 馬体重 | horse_weight | kg |
| 馬体重増減 | delta_weight | kg |
| 騎手複勝率 | jockey_place_ratio | 過去1ヶ月の騎手の複勝率 |
また、決定木とランダムフォレストの実装にはscikit-learn23を使いました。パラメータの決定方法はグリッドサーチで行ないました。決定木は $ max_depth \in {1, 2,…, 7} $ 、 $ min_samples_leaf \in {2, 4, 6,…, 20} $ 、 $ max_leaf_nodes \in {2, 4, 6,…, 50} $ 、ランダムフォレストは $ max_feature \in {1, 2, 3,…, 14} $ 、$ max_leaf_nodes \in {2, 4, 6,…, 50} $ の探索空間に設定しました。また、ランダムフォレストの決定木の数は100に設定しました。
ベースラインの評価
評価のベースラインとして、今回も過去記事と同様に単勝人気順位のTop-N Boxの評価を使います。評価値は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.314 0.717 1.132
place 0.629 0.786 0.616
---- Top-2 BOX
hit ret ret_std
win 0.486 0.680 0.787
place 0.800 0.766 0.466
quinella place 0.314 0.697 1.085
quinella 0.143 0.457 1.168
exacta 0.143 0.527 1.448
---- Top-3 BOX
hit ret ret_std
win 0.543 0.536 0.561
place 0.914 0.754 0.331
quinella place 0.543 0.634 0.765
quinella 0.200 0.250 0.529
exacta 0.200 0.245 0.539
trio 0.086 0.466 1.690
trifecta 0.086 0.253 0.918
---- Top-4 BOX
hit ret ret_std
win 0.686 0.669 0.642
place 0.971 0.746 0.254
quinella place 0.743 0.638 0.609
quinella 0.343 0.405 0.696
exacta 0.343 0.381 0.670
trio 0.171 0.416 1.032
trifecta 0.171 0.292 0.773
---- Top-5 BOX
hit ret ret_std
win 0.800 0.765 0.668
place 0.971 0.741 0.269
quinella place 0.886 0.710 0.642
quinella 0.514 0.608 0.831
exacta 0.514 0.595 0.878
trio 0.314 0.507 1.064
trifecta 0.314 0.513 1.331
複勝圏内確率の予測
Top-N Box 評価
決定木の評価の評価は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.265 0.629 1.136
place 0.618 1.018 1.050
---- Top-2 BOX
hit ret ret_std
win 0.294 0.346 0.578
place 0.676 0.699 0.714
quinella place 0.118 0.585 2.245
quinella 0.029 0.091 0.524
exacta 0.029 0.101 0.583
---- Top-3 BOX
hit ret ret_std
win 0.324 0.358 0.791
place 0.765 0.716 0.566
quinella place 0.412 0.729 1.172
quinella 0.088 0.159 0.560
exacta 0.088 0.125 0.425
trio 0.029 0.129 0.743
trifecta 0.029 0.088 0.507
---- Top-4 BOX
hit ret ret_std
win 0.353 0.301 0.608
place 0.853 0.649 0.397
quinella place 0.529 0.472 0.648
quinella 0.118 0.092 0.286
exacta 0.118 0.077 0.224
trio 0.059 0.132 0.594
trifecta 0.059 0.086 0.384
---- Top-5 BOX
hit ret ret_std
win 0.412 0.311 0.553
place 0.971 0.725 0.400
quinella place 0.647 0.550 0.578
quinella 0.265 0.456 1.743
exacta 0.265 0.396 1.574
trio 0.176 0.151 0.370
trifecta 0.176 0.120 0.352
ランダムフォレストの評価は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.118 0.353 1.065
place 0.618 1.074 1.057
---- Top-2 BOX
hit ret ret_std
win 0.324 0.740 1.577
place 0.824 0.994 0.859
quinella place 0.265 1.544 4.172
quinella 0.088 2.832 11.878
exacta 0.088 2.551 11.328
---- Top-3 BOX
hit ret ret_std
win 0.471 0.659 1.075
place 0.941 0.880 0.672
quinella place 0.412 1.274 3.293
quinella 0.265 1.450 4.134
exacta 0.265 1.240 3.856
trio 0.118 4.312 21.206
trifecta 0.118 2.599 11.414
---- Top-4 BOX
hit ret ret_std
win 0.529 0.581 0.833
place 0.941 0.804 0.517
quinella place 0.676 0.887 1.625
quinella 0.353 0.963 2.222
exacta 0.353 0.848 2.062
trio 0.118 1.078 5.301
trifecta 0.118 0.650 2.854
---- Top-5 BOX
hit ret ret_std
win 0.647 0.661 0.823
place 0.971 0.771 0.415
quinella place 0.765 0.866 1.085
quinella 0.529 0.871 1.389
exacta 0.529 0.804 1.363
trio 0.324 0.925 2.322
trifecta 0.324 0.785 1.770
決定木とランダムフォレストの両方で、線形モデルとSVMで超えられなかったtop-1複勝率60%超えを達成しました。同時に回収率も100%越えているので、人気だけが取れているということではないようです。特にランダムフォレストの方は、Top-2, 3の複勝的中率においてベースラインを超えており、かなり高い精度が出ていることがわかります。
走破タイム予測
予測走破タイムと実際の走破タイム比較
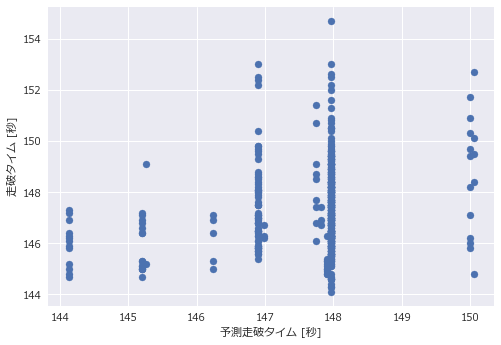
テストデータにおける予測走破タイムと実際の走破タイムをグラフで示します。
まずは決定木(回帰)の結果です。
次にランダムフォレスト(回帰)の結果です。
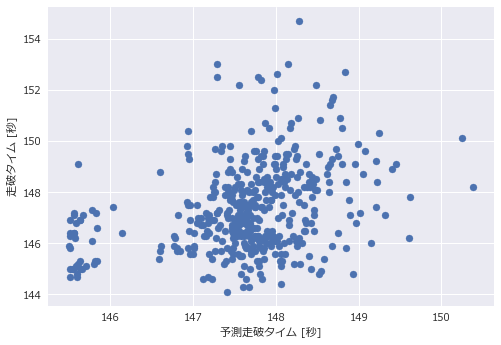
決定木とランダムフォレストのどちらもやや右肩あがりで実際の予測タイムと若干相関しているように見受けられます。決定木のグラフを見てみると、値が離散値になっていることがわかります。これは1本の決定木だとその木の葉の数しか値を表現できないためです。一方ランダムフォレストによる回帰は、全ての木の出力結果を平均するので、値の微妙な違いも表現することが出来ています。
Top-N Box 評価
決定木の評価結果は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.206 0.732 1.858
place 0.500 0.832 1.036
---- Top-2 BOX
hit ret ret_std
win 0.324 0.571 1.087
place 0.647 0.657 0.748
quinella place 0.147 1.306 4.739
quinella 0.059 0.924 4.419
exacta 0.059 0.710 3.423
---- Top-3 BOX
hit ret ret_std
win 0.500 1.021 1.840
place 0.824 0.782 0.611
quinella place 0.382 0.882 1.782
quinella 0.118 0.364 1.478
exacta 0.118 0.288 1.151
trio 0.029 0.129 0.743
trifecta 0.029 0.088 0.507
---- Top-4 BOX
hit ret ret_std
win 0.588 0.886 1.371
place 0.971 0.797 0.484
quinella place 0.529 0.723 1.029
quinella 0.176 0.391 1.197
exacta 0.176 0.317 0.985
trio 0.059 0.132 0.594
trifecta 0.059 0.086 0.384
---- Top-5 BOX
hit ret ret_std
win 0.618 0.768 1.111
place 0.971 0.674 0.429
quinella place 0.618 0.570 0.748
quinella 0.265 0.510 1.180
exacta 0.265 0.521 1.304
trio 0.088 0.209 0.922
trifecta 0.088 0.251 1.250
ランダムフォレストの評価結果は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.235 0.488 0.910
place 0.618 0.994 0.994
---- Top-2 BOX
hit ret ret_std
win 0.353 0.538 0.955
place 0.735 0.806 0.680
quinella place 0.265 1.194 3.409
quinella 0.118 3.318 17.146
exacta 0.118 2.997 15.617
---- Top-3 BOX
hit ret ret_std
win 0.441 0.534 0.826
place 0.882 0.751 0.489
quinella place 0.412 0.657 1.376
quinella 0.147 1.130 5.712
exacta 0.147 1.027 5.203
trio 0.000 0.000 0.000
trifecta 0.000 0.000 0.000
---- Top-4 BOX
hit ret ret_std
win 0.618 0.879 1.302
place 0.941 0.821 0.482
quinella place 0.706 0.735 0.981
quinella 0.353 1.385 3.605
exacta 0.353 1.320 3.490
trio 0.029 0.065 0.376
trifecta 0.029 0.034 0.194
---- Top-5 BOX
hit ret ret_std
win 0.676 0.761 1.033
place 0.971 0.781 0.383
quinella place 0.824 0.774 0.679
quinella 0.500 1.047 2.151
exacta 0.500 0.959 2.075
trio 0.235 0.372 0.784
trifecta 0.235 0.277 0.609
複勝予測と同様に、ランダムフォレストのTop-1複勝的中率は60%を越えています。この評価値も線形モデルとSVMの結果を上回った結果となっています。決定木の精度が低いのは、予測走破タイムのグラフで示したように、回帰木1本が表現できる数値の数が葉の数に限定されるためであると考えられます。その意味でも、多数決をとることがいかに重要であるかということがわかります。
ランダムフォレストで特徴量の重要度をプロットする
ランダムフォレストは決定木を作成するときの分岐による情報利得に基づき、特徴量の重要度が計算できます。複勝分類および走破タイム予測回帰を学習したランダムフォレストの特徴量の重要度は以下の通りです。
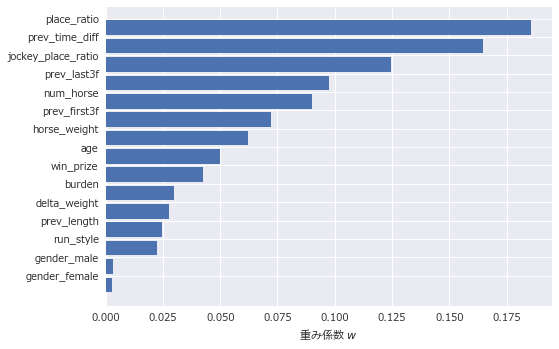
▼ 複勝分類
▼ 走破タイム回帰
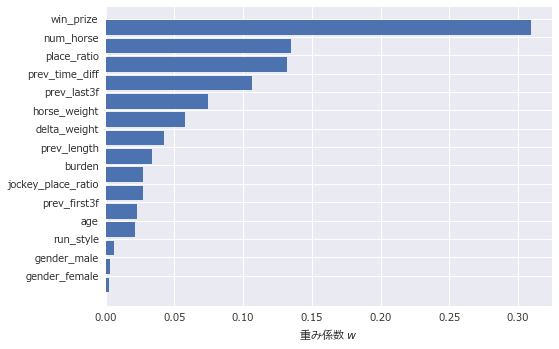
複勝分類ではその馬の複勝率(place_ratio) 、前走の着差 (prev_time_diff) 、騎手の複勝率 (jockecy_place_ratio) が上位にランクしています。やはり複勝に入るかどうかを予想するときは、その馬の複勝率と騎手の複勝率に注目するのが良いのでしょう。一方、走破タイム回帰では、レースの1着賞金 (win_prize) や頭数 (num_horse) といったレースの格や環境の情報が上位にランクしています。タイムは出走馬の能力以上に、どんな環境で走るのかというのが重要であるということを示唆しています。
2016年ジャパンカップを予測する
最後に決定木とランダムフォレストで2016年ジャパンカップの複勝確率と走破タイムを予測してみます。
まず、レース結果は以下の通りです。
| 着順 | 馬番 | 馬名 | 人気 | 走破タイム |
|---|---|---|---|---|
| 1 | 1 | キタサンブラック | 1 | 2:25.8 |
| 2 | 12 | サウンズオブアース | 5 | 2:26.2 |
| 3 | 17 | シュヴァルグラン | 6 | 2:26.3 |
| 4 | 3 | ゴールドアクター | 3 | 2:26.4 |
| 5 | 16 | リアルスティール | 2 | 2:26.4 |
| 6 | 14 | レインボーライン | 8 | 2:26.4 |
| 7 | 5 | イキートス | 16 | 2:26.4 |
| 8 | 7 | ワンアンドオンリー | 14 | 2:26.6 |
| 9 | 4 | ルージュバック | 7 | 2:26.8 |
| 10 | 6 | ラストインパクト | 13 | 2:26.9 |
| 11 | 10 | トーセンバジル | 12 | 2:26.9 |
| 12 | 15 | ナイトフラワー | 9 | 2:26.9 |
| 13 | 9 | ディーマジェスティ | 4 | 2:27.1 |
| 14 | 8 | イラプト | 10 | 2:27.1 |
| 15 | 13 | ヒットザターゲット | 17 | 2:27.2 |
| 16 | 2 | ビッシュ | 11 | 2:27.2 |
| 17 | 11 | フェイムゲーム | 15 | 2:27.3 |
次に決定木とランダムフォレストによる予測複勝確率です。
▼ 決定木(複勝予測)
| 予測順位 | 馬番 | 馬名 | 予測複勝確率 |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 0.875 |
| 2 | 15 | ナイトフラワー | 0.556 |
| 2 | 14 | レインボーライン | 0.556 |
| 2 | 12 | サウンズオブアース | 0.556 |
| 2 | 10 | トーセンバジル | 0.556 |
| 2 | 16 | リアルスティール | 0.556 |
| 2 | 9 | ディーマジェスティ | 0.556 |
| 2 | 4 | ルージュバック | 0.556 |
| 2 | 3 | ゴールドアクター | 0.556 |
| 2 | 2 | ビッシュ | 0.556 |
| 2 | 17 | シュヴァルグラン | 0.556 |
| 12 | 11 | フェイムゲーム | 0.429 |
| 13 | 6 | ラストインパクト | 0.115 |
| 13 | 13 | ヒットザターゲット | 0.115 |
| 15 | 8 | イラプト | 0.071 |
| 15 | 5 | イキートス | 0.071 |
| 15 | 7 | ワンアンドオンリー | 0.071 |
▼ ランダムフォレスト(複勝予測)
| 予測順位 | 馬番 | 馬名 | 予測複勝確率 |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 0.626 |
| 2 | 17 | シュヴァルグラン | 0.623 |
| 3 | 10 | トーセンバジル | 0.622 |
| 4 | 16 | リアルスティール | 0.620 |
| 5 | 3 | ゴールドアクター | 0.618 |
| 6 | 14 | レインボーライン | 0.610 |
| 7 | 12 | サウンズオブアース | 0.596 |
| 8 | 9 | ディーマジェスティ | 0.577 |
| 9 | 2 | ビッシュ | 0.574 |
| 10 | 4 | ルージュバック | 0.570 |
| 11 | 15 | ナイトフラワー | 0.559 |
| 12 | 6 | ラストインパクト | 0.506 |
| 13 | 7 | ワンアンドオンリー | 0.498 |
| 14 | 8 | イラプト | 0.470 |
| 15 | 5 | イキートス | 0.417 |
| 16 | 11 | フェイムゲーム | 0.401 |
| 17 | 13 | ヒットザターゲット | 0.356 |
▼ 決定木 (走破タイム予測)
| 予測順位 | 馬番 | 馬名 | 予測タイム |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 2:23.40 |
| 1 | 12 | サウンズオブアース | 2:23.40 |
| 1 | 11 | フェイムゲーム | 2:23.40 |
| 1 | 10 | トーセンバジル | 2:23.40 |
| 5 | 9 | ディーマジェスティ | 2:24.68 |
| 5 | 3 | ゴールドアクター | 2:24.68 |
| 7 | 16 | リアルスティール | 2:25.07 |
| 7 | 13 | ヒットザターゲット | 2:25.07 |
| 7 | 17 | シュヴァルグラン | 2:25.07 |
| 10 | 6 | ラストインパクト | 2:25.37 |
| 10 | 7 | ワンアンドオンリー | 2:25.37 |
| 10 | 4 | ルージュバック | 2:25.37 |
| 10 | 2 | ビッシュ | 2:25.37 |
| 10 | 14 | レインボーライン | 2:25.37 |
| 15 | 5 | イキートス | 2:25.98 |
| 16 | 8 | イラプト | 2:27.43 |
| 16 | 15 | ナイトフラワー | 2:27.43 |
▼ ランダムフォレスト (走破タイム予測)
| 予測順位 | 馬番 | 馬名 | 予測タイム |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 2:25.45 |
| 2 | 16 | リアルスティール | 2:25.47 |
| 3 | 12 | サウンズオブアース | 2:25.49 |
| 4 | 10 | トーセンバジル | 2:25.50 |
| 5 | 17 | シュヴァルグラン | 2:25.50 |
| 6 | 3 | ゴールドアクター | 2:25.55 |
| 7 | 9 | ディーマジェスティ | 2:25.58 |
| 8 | 4 | ルージュバック | 2:25.59 |
| 9 | 6 | ラストインパクト | 2:25.64 |
| 10 | 14 | レインボーライン | 2:25.65 |
| 11 | 2 | ビッシュ | 2:25.66 |
| 12 | 15 | ナイトフラワー | 2:25.69 |
| 13 | 8 | イラプト | 2:25.80 |
| 14 | 11 | フェイムゲーム | 2:25.84 |
| 15 | 13 | ヒットザターゲット | 2:25.97 |
| 16 | 7 | ワンアンドオンリー | 2:26.07 |
| 17 | 5 | イキートス | 2:26.15 |
まず、決定木による複勝予測、走破タイム予測のいずれにおいても、同スコアの馬が多く存在します。決定木は数値を離散的に扱っている性質上、確率やタイムのような連続値を表現するには不向きであることがわかります。
一方、ランダムフォレストでは同スコアの馬は見当たりません。予測の中身を見てみると、複勝予測ではキタサンブラックが1着にとれているだけでなく、3着に入線したシュヴァルグラン (6人気) が2番手に評価されています。Top-N 評価の定量評価が示唆していた通り、人気ではないが複勝圏内に入ってくる馬の特量を学習しているのだと考えられます。タイム予測の方でも1位評価がキタサンブラック、3位評価にサウンズオブアースと良い予測になっています。このように、ランダムフォレストは分類でも回帰でも良い性能が出る有能なアルゴリズムであり、巷で人気があるのも頷けるでしょう。
おわりに
今回は決定木とそれをアンサンブルしたランダムフォレストの2つを紹介しました。実験結果から、ランダムフォレストがいかに強力なアルゴリズムであるかということがおわかりいただけたかと思います。
これまでの解説の中で既に気がついた人がいるかもしれませんが、オッズは全国の馬券購入者の予想の集合知であり、馬券購入者のアンサンブルです。馬券購入者は各々自分が重視しているファクター (特徴量) で予想しており、記憶にあるレースも各々異なるため、ランダムフォレストとかなり近いことをしていると言えるでしょう。オッズ(人気)の的中率が高いのはそのためです。
次回は理論記事はお休みにして特別記事を書く予定です。お楽しみに。
-
「ある事柄を説明するためには、必要以上に多くを仮定するべきではない」とする原則 ↩︎
-
決定木に使用したライブラリ: DecisionTreeClassifier DecisionTreeRegressor ↩︎
-
ランダムフォレストに使用したライブラリ: RandomForestClassifier RandomForestRegressor ↩︎