第8回の理論記事では線形回帰と一般化線形モデルの一種であるロジスティック回帰による競馬予測に挑戦します。
線形回帰
走破タイムや着順といった結果を予測するためには、1つのファクターだけに注目するのは不十分で、複数のファクターから受ける影響を同時に考える必要があります。それを実現する最も簡単な方法が、以下のように走破タイムなどの目的変数 $ y $ を特徴量(説明変数)の線形和として表す線形回帰モデルです。
$$ y = w_0 + w_1 x_1 + … + w_m x_m = \mathbf{w}^T \mathbf{x}$$
特徴量の数が1つの場合は単回帰、複数の場合は重回帰と呼ばれます。線形モデルの強みは、各特徴量に対応する重み $ w_i $ を見ることでその特徴量がプラスに働いているか、マイナスに働いているか、影響がないのかということを簡単に判別できるということです。その一方で、目的変数と特徴量が線形の関係にあること、特徴量同士は独立した変数であることなどの仮定がおかれているため、特徴量選びや白色化などの前処理に注意しなければなりません。そうとはいえ、まず回帰問題を解くというときは最も簡単な線形モデルを使うのが常套手段でしょう。
学習のためのコスト関数は一般に以下で表される平均二乗誤差が使われます。
$$ L(\mathbf{w}) = \frac{1}{N}\sum_{n=1}^{N} (y_n -\mathbf{w}^T \mathbf{x_n})^2 $$
このコスト関数を最小化する $ \mathbf{w} $ を探索することで、未知の特徴ベクトルに対する予測性能が生まれます。
ロジスティック回帰
典型的な競馬予測では馬が勝つか/負けるか、馬券内に入ったかどうかなどの2値分類問題として表すことができます。そのような0/1の確率問題を、線形モデルを一般化して解く代表的な方法がロジスティック回帰です。ロジスティック回帰は回帰という名前がついていますが、これは $ (0, 1) $ の範囲で確率を回帰するという意味なので、あくまでも分類器です。線形関数 $ z=\mathbf{w}^T\mathbf{x} $ は $ (-\infty, \infty) $ の範囲をとり、そのままでは確率として扱えません。そこでロジスティック回帰では、以下のシグモイド関数による非線形変換を施すことにより $ (0, 1) $ の確率の範囲に変換します。
$$\sigma(z)=\frac{1}{1 + \exp(-z)}$$
シグモイド関数をプロットすると以下のような曲線となります。
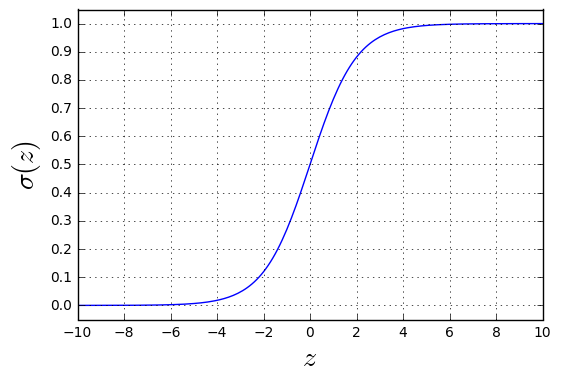
このグラフの横軸がシグモイド関数の入力となる $ z = \mathbf{w}^T\mathbf{x} $ 、縦軸がそれに対応するシグモイド関数による確率を表しています。上のグラフからわかるように、シグモイド関数は $ z=0 $ で確率の分布が対称となっています。ロジスティック回帰を使った競馬予測では、シグモイド関数 $ \sigma(z) $ を1着になる確率や馬券内に入る確率と定義して、訓練データのレース結果の生起確率が尤もらしくなる重みパラメータ $ \mathbf{w} $ を学習します。こうして学習した重みにより計算された $ z=\mathbf{w}^T\mathbf{x} $ が正の値をとった場合は50%以上の確率で1着(馬券内)、負の値をとったときは負け(馬券外)と解釈できます。
最小化するコスト関数は以下で表される交差エントロピーが用いられます。
$$ L(\mathbf{w}) = \frac{1}{N} \sum_{n=1}^{N} - (y_n \log{\sigma(z_n)} + (1 - y_n) \log{(1 - \sigma(z_n))}$$
ただし、 $ y_n $ は $ n $ 番目のサンプルの正解ラベルで $ {0, 1} $ のいずれかの値が入ります。この式の特徴は、 $ y_n = 1 $ の場合、 $ \sigma(z_n) = 1 $ となるときにコスト関数が最小となり、反対に $ y_n = 0 $ の場合、 $ \sigma(z_n) = 0 $ となるときにコスト関数の値が最小となります。そのため勝ち馬かどうかの二値分類問題では、交差エントロピーを最小化することにより、勝ち馬の特徴ベクトルを持った馬の予測勝利確率が高くなるような重みパラメータの学習がなされます。
実験設定
今回は東京芝2,400mの古馬戦の条件で実際に競馬予測を行っていきます。線形回帰では走破タイム予測、ロジスティック回帰では複勝圏内に入るかどうかの2値分類タスクを解きます。評価方法は前回の記事で紹介した通りTop-1からTop-5までのBox買いの的中率・回収率で比較します。
訓練に使ったレースは2010年2014年の5年間に行われた当該条件レース(121レース)、評価用のテストデータは20152016年の2年間のレース(35レース)とします。また、キタサンブラックが優勝した2016年ジャパンカップで定性評価を行ないます1。
今回使用した特徴量は以下の通りです。
| 特徴量名 | カラム名 | 説明 |
|---|---|---|
| 出走頭数 | num_horse | レースに出走する頭数 |
| 1着賞金 | win_prize | レースレベルの指標 |
| 馬齢 | age | 馬の年齢 |
| 性別 | gender | 牡・牝のダミー変数(騙馬は少ないのでダミー変数にしない) |
| 斤量 | burden | kg |
| 脚質 | run_style | 逃げ=1, 先行=2, 差し=3, 追込=4 |
| 馬複勝率 | place_ratio | 馬の通算複勝率 |
| 前走距離 | prev_length | メートル |
| 前走タイム差 | prev_time_diff | 1着との秒差 |
| 前走前3Fタイム | prev_first3f | 秒 |
| 前走後3Fタイム | prev_last3f | 秒 |
| 馬体重 | horse_weight | kg |
| 馬体重増減 | delta_weight | kg |
| 騎手複勝率 | jockey_place_ratio | 過去1ヶ月の騎手の複勝率 |
各特徴量はスケールが大きく異なるため、平均0、分散1になるように標準化をして各モデルへの入力とします。また、モデルのパラメータはscikit-learnのデフォルト値としました23。
線形回帰によるタイム予測
予測走破タイムと実際の走破タイム比較
テストデータにおける予測走破タイムと実際の走破タイムの結果は以下の図のようになりました。
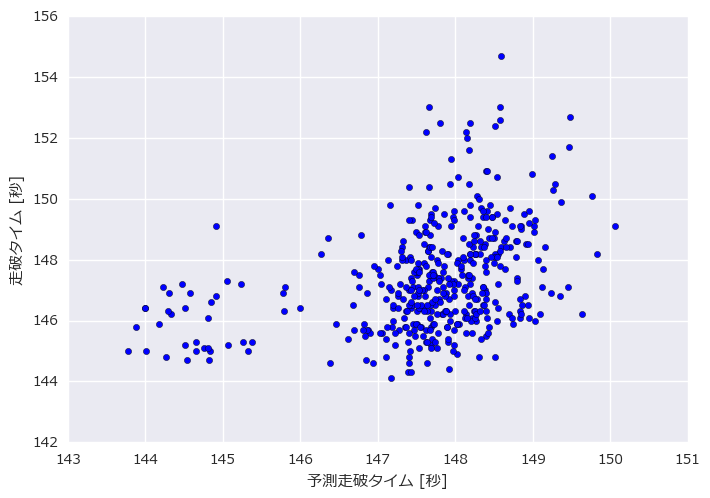
もしも完璧にタイムが予測できている場合は綺麗な斜め45度の直線になります。このグラフを見ると完璧には程遠いですが、予測タイムが速くなるにつれて実際の走破タイムも若干速くなっている傾向は見受けられ、何かしら意味のある予測が出力されているように見えます。
Top-N Box 評価
Top-N BOXのモデルの性能は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.235 1.335 4.273
place 0.529 0.897 1.096
---- Top-2 BOX
hit ret ret_std
win 0.382 1.043 2.343
place 0.765 0.960 0.819
quinella place 0.265 1.159 2.943
quinella 0.118 0.421 1.228
exacta 0.118 0.376 1.074
---- Top-3 BOX
hit ret ret_std
win 0.500 0.853 1.567
place 0.882 0.858 0.553
quinella place 0.441 0.832 1.368
quinella 0.235 0.747 1.984
exacta 0.235 0.782 2.311
trio 0.059 0.685 2.904
trifecta 0.059 0.584 2.638
---- Top-4 BOX
hit ret ret_std
win 0.529 0.714 1.212
place 0.941 0.740 0.409
quinella place 0.529 0.680 0.958
quinella 0.235 0.374 0.992
exacta 0.235 0.391 1.155
trio 0.118 0.443 1.395
trifecta 0.118 0.284 0.887
---- Top-5 BOX
hit ret ret_std
win 0.618 0.700 1.037
place 0.971 0.752 0.444
quinella place 0.676 0.849 1.100
quinella 0.441 0.661 1.299
exacta 0.441 0.600 1.278
trio 0.265 0.817 2.242
trifecta 0.265 0.500 1.254
また、ベースライン(確定単勝人気)の評価は以下の通りです。
---- Top-1 BOX
hit ret ret_std
win 0.314 0.717 1.132
place 0.629 0.786 0.616
---- Top-2 BOX
hit ret ret_std
win 0.486 0.680 0.787
place 0.800 0.766 0.466
quinella place 0.314 0.697 1.085
quinella 0.143 0.457 1.168
exacta 0.143 0.527 1.448
---- Top-3 BOX
hit ret ret_std
win 0.543 0.536 0.561
place 0.914 0.754 0.331
quinella place 0.543 0.634 0.765
quinella 0.200 0.250 0.529
exacta 0.200 0.245 0.539
trio 0.086 0.466 1.690
trifecta 0.086 0.253 0.918
---- Top-4 BOX
hit ret ret_std
win 0.686 0.669 0.642
place 0.971 0.746 0.254
quinella place 0.743 0.638 0.609
quinella 0.343 0.405 0.696
exacta 0.343 0.381 0.670
trio 0.171 0.416 1.032
trifecta 0.171 0.292 0.773
---- Top-5 BOX
hit ret ret_std
win 0.800 0.765 0.668
place 0.971 0.741 0.269
quinella place 0.886 0.710 0.642
quinella 0.514 0.608 0.831
exacta 0.514 0.595 0.878
trio 0.314 0.507 1.064
trifecta 0.314 0.513 1.331
的中率は人気には及ぼないものの評価1番手の単勝で23%ほどが的中しているので予測はできているようです。回収率は133.5%ありますが回収率の標準偏差が4.2と大きめなのでコンスタントに穴を当てているというよりは大きな当たりを一度出していると読み取れます。
特徴量の重み係数
各特徴量の重み係数は以下のようになりました。
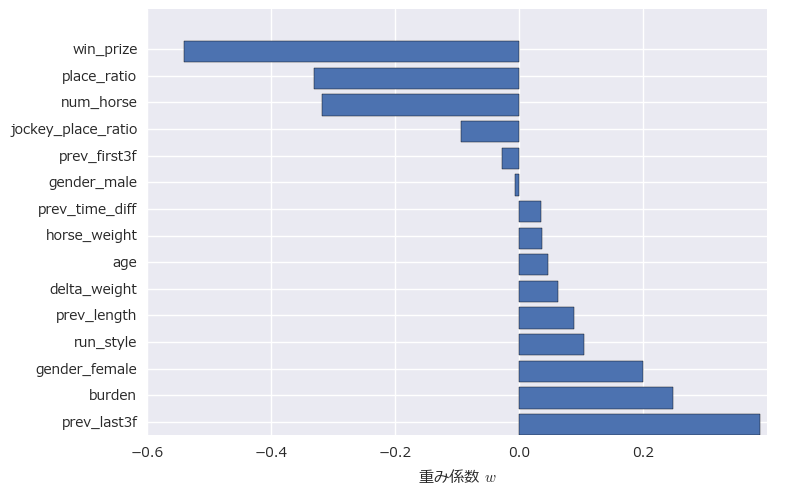
このグラフの上にある特徴量の値が大きいほどタイムが速くなり、下にある特徴量の値が大きいほどタイムが遅くなることを表しています。レースの格を表す1着賞金(win_prize)が最上位に来るのは直感にあっていると思います。また出走頭数が多いほどハイペースになりやすいので、出走頭数(num_horse)が上位にきているのも納得のいく結果です。馬体重(horse_weight)や年齢(age)などはベスト値にピークがあり、大きければ大きいほど(小さければ小さいほど)良いというわけではなく線形性がないので、線形モデルでは予測結果に効いてこないのだと考えられます。
ロジスティック回帰による複勝圏内確率の予測
Top-N Box 評価
---- Top-1 BOX
hit ret ret_std
win 0.235 0.532 1.026
place 0.559 0.738 0.683
---- Top-2 BOX
hit ret ret_std
win 0.324 0.415 0.652
place 0.765 0.737 0.532
quinella place 0.235 0.491 0.926
quinella 0.088 0.250 0.807
exacta 0.088 0.285 0.920
---- Top-3 BOX
hit ret ret_std
win 0.382 0.381 0.570
place 0.824 0.651 0.449
quinella place 0.382 0.556 0.989
quinella 0.176 0.580 1.738
exacta 0.176 0.508 1.450
trio 0.059 0.526 2.378
trifecta 0.059 0.343 1.535
---- Top-4 BOX
hit ret ret_std
win 0.588 0.626 0.970
place 0.941 0.779 0.404
quinella place 0.706 0.779 0.995
quinella 0.353 0.859 1.653
exacta 0.353 0.818 1.720
trio 0.147 0.635 2.065
trifecta 0.147 0.704 2.775
---- Top-5 BOX
hit ret ret_std
win 0.647 0.698 1.022
place 0.941 0.728 0.368
quinella place 0.765 0.762 0.911
quinella 0.471 0.771 1.184
exacta 0.471 0.776 1.350
trio 0.294 0.751 1.678
trifecta 0.294 0.841 1.858
ベースライン、タイム予測の線形回帰に比べると全体的に成績があまり良くない傾向があります。回収率もあまり高くないのは的中している馬券のほとんどが人気サイドであることを示唆しています。
特徴量の重み係数
各特徴量の重み係数は以下のようになりました。
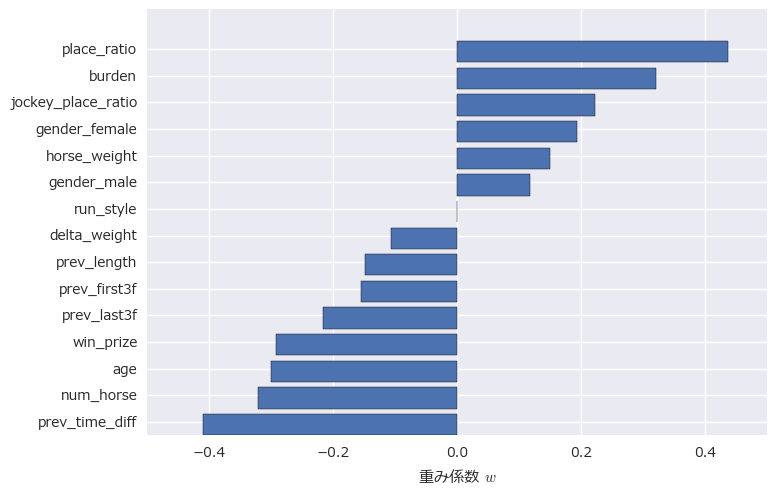
このグラフの上位の特徴量の値が大きいほど複勝確率が高く、下位の特徴量の値が大きいほど複勝確率が低いことを表しています。複勝確率はやはりその馬の複勝率(place_ratio)が最も効くというわかりやすい結果となりました。また騎手の複勝率(jockey_place_ratio)も重要なファクターのようです。また意外なことに、古馬東京2,400m戦では牝馬(gender_female)であることが大きなプラス材料となっています。たしかに近年のジャパンカップではウオッカ、ブエナビスタ、ジェンティルドンナ、ショウナンパンドラなどの牝馬の活躍が目立っているので、それがしっかりと反映されているのでしょう。
2016年ジャパンカップを予測する
最後に線形回帰とロジスティック回帰で2016年ジャパンカップを予測してみます。
まず、レース結果は以下の通りです。
| 着順 | 馬番 | 馬名 | 人気 | 走破タイム |
|---|---|---|---|---|
| 1 | 1 | キタサンブラック | 1 | 2:25.8 |
| 2 | 12 | サウンズオブアース | 5 | 2:26.2 |
| 3 | 17 | シュヴァルグラン | 6 | 2:26.3 |
| 4 | 3 | ゴールドアクター | 3 | 2:26.4 |
| 5 | 16 | リアルスティール | 2 | 2:26.4 |
| 6 | 14 | レインボーライン | 8 | 2:26.4 |
| 7 | 5 | イキートス | 16 | 2:26.4 |
| 8 | 7 | ワンアンドオンリー | 14 | 2:26.6 |
| 9 | 4 | ルージュバック | 7 | 2:26.8 |
| 10 | 6 | ラストインパクト | 13 | 2:26.9 |
| 11 | 10 | トーセンバジル | 12 | 2:26.9 |
| 12 | 15 | ナイトフラワー | 9 | 2:26.9 |
| 13 | 9 | ディーマジェスティ | 4 | 2:27.1 |
| 14 | 8 | イラプト | 10 | 2:27.1 |
| 15 | 13 | ヒットザターゲット | 17 | 2:27.2 |
| 16 | 2 | ビッシュ | 11 | 2:27.2 |
| 17 | 11 | フェイムゲーム | 15 | 2:27.3 |
次に、線形回帰による予測走破タイムです。
| 予測順位 | 馬番 | 馬名 | 予測タイム |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 2:23.9 |
| 2 | 14 | レインボーライン | 2:24.0 |
| 3 | 16 | リアルスティール | 2:24.0 |
| 4 | 9 | ディーマジェスティ | 2:24.2 |
| 5 | 17 | シュヴァルグラン | 2:24.3 |
| 6 | 10 | トーセンバジル | 2:24.3 |
| 7 | 12 | サウンズオブアース | 2:24.3 |
| 8 | 2 | ビッシュ | 2:24.5 |
| 9 | 3 | ゴールドアクター | 2:24.5 |
| 10 | 6 | ラストインパクト | 2:24.6 |
| 11 | 7 | ワンアンドオンリー | 2:24.8 |
| 12 | 4 | ルージュバック | 2:24.9 |
| 13 | 11 | フェイムゲーム | 2:25.1 |
| 14 | 13 | ヒットザターゲット | 2:25.2 |
| 15 | 15 | ナイトフラワー | 2:25.8 |
| 16 | 8 | イラプト | 2:25.8 |
| 17 | 5 | イキートス | 2:26.0 |
最後に、ロジスティック回帰による予測複勝確率です。
| 予測順位 | 馬番 | 馬名 | 予測複勝確率 |
|---|---|---|---|
| 1 | 1 | キタサンブラック | 0.7 |
| 2 | 16 | リアルスティール | 0.7 |
| 3 | 12 | サウンズオブアース | 0.6 |
| 4 | 3 | ゴールドアクター | 0.5 |
| 4 | 17 | シュヴァルグラン | 0.5 |
| 4 | 14 | レインボーライン | 0.5 |
| 7 | 10 | トーセンバジル | 0.4 |
| 7 | 6 | ラストインパクト | 0.4 |
| 7 | 9 | ディーマジェスティ | 0.4 |
| 7 | 4 | ルージュバック | 0.4 |
| 11 | 2 | ビッシュ | 0.3 |
| 11 | 15 | ナイトフラワー | 0.3 |
| 11 | 7 | ワンアンドオンリー | 0.3 |
| 14 | 8 | イラプト | 0.2 |
| 15 | 13 | ヒットザターゲット | 0.1 |
| 15 | 11 | フェイムゲーム | 0.1 |
| 15 | 5 | イキートス | 0.1 |
線形回帰でもロジスティック回帰でもキタサンブラックを最上位に推薦できています。タイム予測では実際のタイムよりも速いタイムとなっていますが、キタサンブラックを最上位に評価できていることがわかります。ロジスティック回帰では定量評価はあまり結果が良くなかったものの、馬券内に絡んだ3頭をトップ6までに全頭推薦できています。
ちなみに2016年ジャパンカップ当時のAlphaImpactが出した予測を見てみると、フェイムゲームやらヒットザターゲットやら結果的に大敗している大穴ばかりを狙っており、見境の無いギャンブラーのような予測をしていました。しかし、この結果は開発者にニューラルネットの"気持ち"を伝え、以降の飛躍的な精度向上のきっかけとなりました。この話はいずれ理論解説で触れたいと思います。
おわりに
今回は線形回帰とロジスティック回帰で競馬予測を試してみましたが、ベースラインの壁を越えるのはこれだけでは足らないようです。しかしキタサンブラックをちゃんと取れていたことは評価したいと思います。
次回は非線形モデルの代表格サポートベクターマシン(SVM)による競馬予測に挑戦したいと思います。2016年ジャパンカップの定性評価は今後も続きます。お楽しみに。
-
AlphaImpactでは当時の競馬AIが圧倒的強さで勝ったキタサンブラックを低評価してしまった悔しさから、2016年ジャパンカップをよく定性評価レースとして使うようになった。 ↩︎
-
線形回帰に使用したライブラリ: sklearn.linear_model.LinearRegression ↩︎
-
ロジスティック回帰に使用したライブラリ: sklearn.linear_model.LogisticRegression ↩︎