今回は今週末開催される宝塚記念の出走予定馬のコース適性を、非負値行列因子分解を利用して分析していきます。
非負値行列因子分解 (Non-negative Matrix Factorization, NMF)
非負値行列因子分解(NMF)は非負値のデータ行列 $ \mathbf{X} $ を低ランクの非負値行列 $ \mathbf{W} $ , $ \mathbf{H} $ の積として近似する次元削減手法です。式にすると以下のように表せます。
$$\mathbf{X} \simeq \mathbf{W}\mathbf{H} \\\\mathbf{X} \in \mathbb{R}^{M \times N}_{+},\mathbf{W} \in \mathbb{R}^{M \times K}_{+},\mathbf{H} \in \mathbb{R}^{K \times N}_{+} \tag{1}$$
NMFは、画像や音声、グラフなどの非構造化データからの特徴抽出やアイテムのレコメンドなどに利用される応用範囲の広い教師なし学習手法です。NMFは以下で表されるFrobeniusノルムを最小化するような非負値行列 $ \mathbf{W} $ , $ \mathbf{H} $ を探索する最適化問題として定式化されます。
$$ L = ||\mathbf{X} - \mathbf{W}\mathbf{H}||_{F}^{2} \tag{2}$$
また、損失関数としてはFrobeniusノルム以外にもKullback-Leibler divergenceが用いられる場合もあります。
NMFでコース適性を抽出する
NMFの入力として、以下のように $ X_{ij} $ が馬 $ i $ のコース $ j $ における成績が入っている行列を考えます。今回は成績の指標として、そのコースでの複勝率を用いるとします。また、該当箇所の出走履歴が存在しないところは0埋めします。

この行列に対してNMFを実行すると、以下のような2つの行列に分解されます。
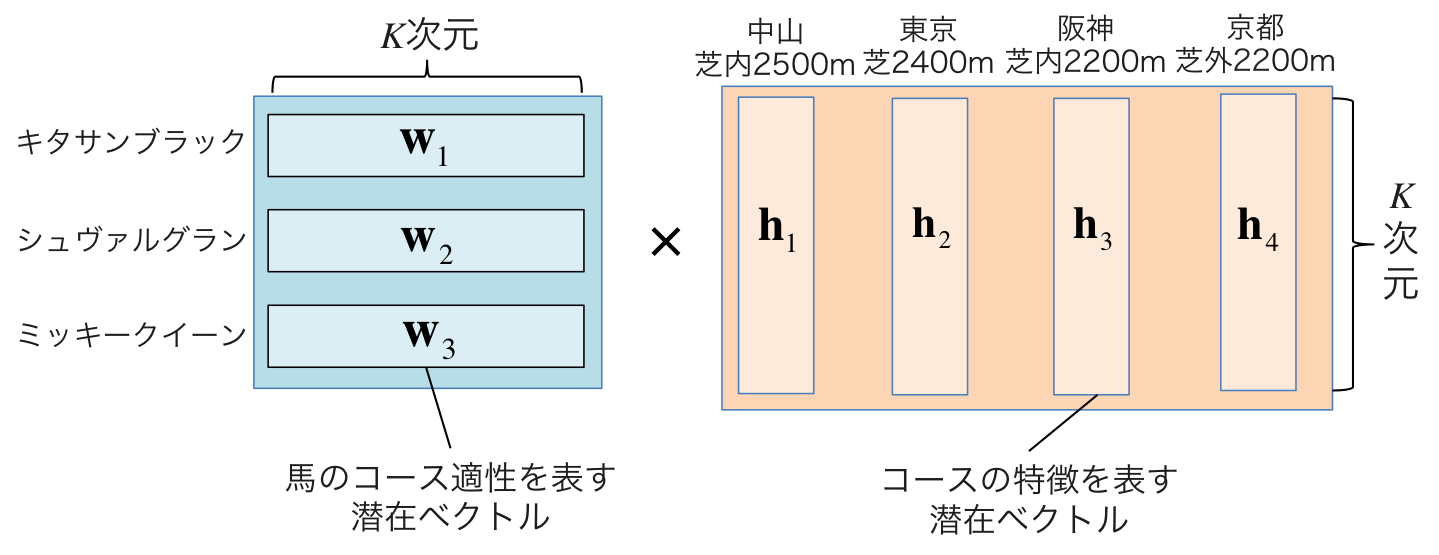
行列 $ \mathbf{W} $ の各行は、対応する馬のコース適性を抽象化した特徴ベクトルになります。一方、行列 $ \mathbf{H} $ の各列は、対応するコースの特徴を抽象化した特徴ベクトルとなります。このような抽象的なベクトル表現を得ることで、似ているコース適性を持つ馬の情報や似ている特徴を持つコースの情報を間接的に利用できるため、過去に走ったことがないコースだとしても、適性度の計算が可能となります。
馬 $ i $ のコース $ j $ に対する適性度のスコア $ s_{ij} $ は潜在ベクトルの内積として以下の式のように表されます。
$$ s_{ij} = \mathbf{w}_i\mathbf{h}_j \tag{3}$$
コース適性の学習
今回は2017年宝塚記念のコース適性を計算することを念頭におき、2013年1月1日~2017年6月18日に行われた芝1600m以上の全レースのデータ(15165頭, 50コース)を学習データに使用します。そのデータから(馬, コース)ごとの複勝率を計算し、入力のデータ行列を作成します。該当データがない行列の要素は0とします。
また、NMFの実装はscikit-learnを利用し、潜在ベクトルの次元数は $ K=5 $ としました。
コース特徴の可視化
NMFにより抽出した5次元のコースの潜在ベクトルを、多次元尺度法であるt-SNEにより2次元平面に投射して可視化した結果を以下に示します。

5次元のベクトルを無理やり2次元に押し込めているので全てが正確ではありませんが、阪神芝内2200mの付近に京都芝外2200mや阪神芝外2400mが位置しているなど、なんとなく似ているコースが近い場所に位置しているように見えます。このように潜在ベクトルを可視化してみるだけでも、似ているコースかどうかが直感的に理解できるので、予想の材料として利用することができそうです。
宝塚記念記念出走馬のコース適性度
2017年宝塚記念に特別登録している11頭の、阪神芝内2200mの適性スコアを算出した結果を以下に示します。
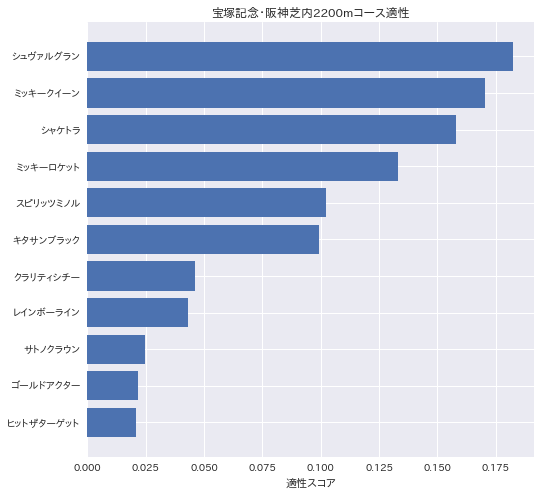
最もコースの適性スコアが高かったのは、天皇賞(春)2着馬のシュヴァルグランでした。阪神芝内2200mで複勝圏内に入ったことがないものの、阪神・京都の芝2000m、2400mでの競走実績が高いので、たしかにコースとの相性は良さそうです。スコア2位のミッキークイーンは、阪神1800~2000mや京都芝外2200mのレースで複勝圏内に入った実績が評価されたのだと考えられます。スコア3位のシャケトラは1000万下条件ながら、当該コースで1着になっている実績があるため、高評価されていると考えられます。
一方、春古馬3冠が期待されているキタサンブラックは意外にも適性スコアは6番手という結果でした。これはおそらく天皇賞(春)や菊花賞での実績があるため、長距離の適性にとられているのかもしれません。コースの潜在ベクトルを可視化した図を見てみると、京都の芝3000m、3200mと阪神芝内2200mは離れた位置にあります。常識的な強さの馬ならば、3000~3200mの長距離が得意な馬が2200mの中距離が強いことはないだろう、といったところでしょうか。
まとめ
NMFは画像・音声処理やレコメンドに使われるイメージが強い手法ですが、入力データを馬×コースの行列とすることによって、コース適性分析に応用できることを紹介しました。2017年宝塚記念のコース適性分析では、
- シュヴァルグラン
- ミッキークイーン
- シャケトラ
の3頭が特に阪神芝内2200mのコース適性度が高いという結果となりました。
また、AlphaImpactの予測エンジンが出した宝塚記念の予測も週末に公開予定ですので、是非そちらとも見比べてみて下さい。