第7回目の理論記事では競馬をどのように機械学習問題に落とし込むのか、また学習した予測モデルの性能評価方法について説明していきます。
教師あり学習と教師なし学習
機械学習の問題は**教師あり学習(Supervised Learning)と教師なし学習(Unsupervised Learning)**の大きく2つに分類されます1。
教師あり学習とは、特徴ベクトル $ \mathbf{x}_i $ に対する望ましい応答 $ y_i $ の組 $ {(\mathbf{x}_i, y_i) } $ を訓練データとして与え、それをガイドにして関係 $ y = f(\mathbf{x}) $ を学習をします。そのようにして得られた予測モデル $ f $ に未知の特徴ベクトルを与えることで未来の現象を予測します。予測モデル $ f $ は、線形モデル、ニューラルネットワーク、決定木、サポートベクターマシンなどモデル種類によって具体的な形は異なります。
また、応答変数 $ y_i $ が勝ち/負けのような2値ラベルなら二値分類問題、1着/2着/3着/着外のような複数のラベルなら多クラス分類問題、走破タイムのような実数値なら回帰問題となります。競馬予測においてどの問題が最適なのかという答えはありませんが、重要なのは入力となる特徴ベクトル $ \mathbf{x}_i $ と応答変数 $ y_i $ の間に規則性が存在し、予測が可能な問題を設定することです。
一方、教師なし学習では教師あり学習のような正解例は与えられず、特徴ベクトルの集合 $ {\mathbf{x}_i} $ のみから学習をします。教師なし学習の代表的な手法がクラスタリングです。クラスタリングとはデータを似ているグループに分割するアルゴリズムです。競馬予測に直接使うことは難しいですが、コース適性が類似している競走馬にグループ分けをしたり、騎乗依頼関係が類似している騎手をグループ分けするなど、データの分析や教師あり学習アルゴリズムへの入力データ作りとして応用することができます。競馬データのクラスタリングはそれだけで記事が丸々書ける面白いテーマなので、今後の理論記事の中で改めて紹介していきたいと思います。
記事の残りのパートでは競馬予測の基本となる教師あり学習について詳しくみていきます。
分類問題で競馬予測
分類問題はデータをあらかじめ定義されているクラスラベルのいずれかに分類するタスクです。競馬予測として考えられる分類問題は以下のような例があります。
- 1着かどうかの予測
- 複勝圏内かどうかの予測
- 1着からの着差が0.1秒以内かどうかの予測
- 1着/2着/3着/着外の予測
- 着順上位(1
3着)/中位(47着)/下位(8~)の予測
問題例の上3種類はクラスラベルがTrue/Falseの2つで表される二値分類問題、下2種類は多クラス分類問題となっています。どの分類問題が競馬予測に優れているかというのは一概には言えませんが、注意しておかないといけないのが訓練データにおけるクラスラベルの不均衡です。訓練データに含まれるサンプルのうちTrueラベルがFalseラベルに比べて極端に少ないと多くのモデルではうまく学習することができません(逆もまたしかり)。
不均衡を解消する一般的な方法として、多い方のクラスラベルを持つサンプルを減少させる方法がありますが、そこまで多いとは言えない貴重な競馬データの学習サンプルを減少させるのはもったいないことです。そのため、できるだけはじめから不均衡ではない問題設定を選ぶことは重要です。だからとはいえ1-8着をTrue、9着以下をFalseなどと極端な分け方をしてしまうと、本当に強い馬の特徴が見えなくなってしまうので、実験を重ねてベストな問題設定を探っていくことになるでしょう。
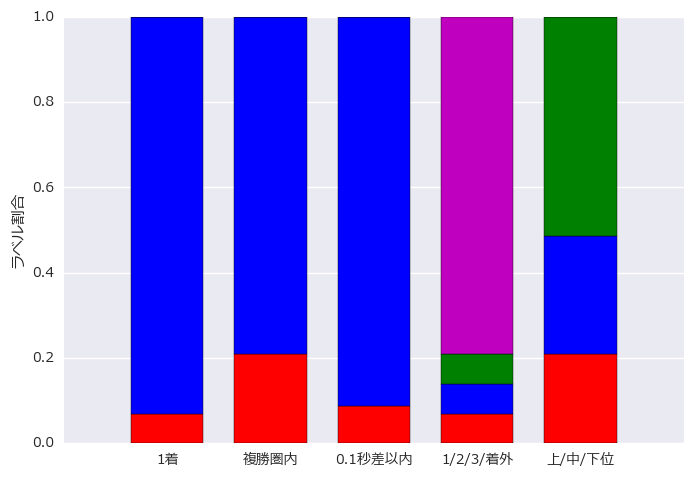
上の各問題におけるクラスラベルの割合を以下の図に示します。1着かどうかの二値分類問題が最もクラスラベルがアンバランスとなっています。上/中/下位の多クラス分類がラベルの均衡に関しては最もバランスが良いことがわかります。
回帰問題で競馬予測
回帰問題は特徴ベクトルから実数値を予測するタスクです。競馬予測として考えられる回帰問題は以下のような例があります。
- 走破タイムの予測
- 走破速度の予測
- スピード指数の予測
- 着順の予測
回帰で一番自然なアプローチが走破タイムの予測でしょう。ただ走破タイムはコース距離によって値が大きく変わるため、異なる距離のレースを同じ訓練データに含めて学習するのは難しい問題設定といえるでしょう。そこで、走破タイムをそのまま予測するのではなく、コースの距離で割った走破速度を予測する回帰問題も考えられます。JRA-VANが提供しているデータマイニング予測のタイム型モデルも走破速度の回帰を解いているようです。
スピード指数の回帰は走破タイムの回帰と似ていますが、スピード指数は馬場差などの外的要因を排除しているため、理想的には馬のパフォーマンスの高さを回帰していることになります。また、着順は多クラス分類問題として考えることもできますが、“2.7着"のような実数値として扱うことを許せば一応回帰として解くことも可能です。
モデルの評価方法
同じ分類・回帰問題を解いていても、モデルの学習で予め設定しなければならないハイパーパラメータや各特徴量を入れるべきかどうかといった調整はモデル性能に大きく影響します。そのときにどのハイパーパラメータが良いか、どの特徴量は入れるべきなのかということを最終判断するためには予測モデルの良し悪しの基準を明確に決めておく必要があります。そこで競馬予測におけるモデルの評価方法について説明していきます。
一般的な分類モデルの評価では正確度(Accuracy)やF値(F-measure)、回帰問題では平均二乗誤差(Mean Squared Error, MSE)が良く使われますが、異なる種類のモデル間で性能の良し悪しを判断するためには競馬予測に共通して使える評価指標が必要となります。
競馬予測において知りたいことは「出走馬1頭(サンプル)が勝つかどうか」というsample-wiseの予測ではなく「あるレースに出走する出走馬の中でどの馬が勝つのか」というrace-wiseの予測です。前者の考え方は絶対評価になるので、もし出走馬のレベルが高い場合は全頭が勝ち馬であると予測するのを許すことになりますが、それは現実の競馬予想に当てはめればナンセンスなのは明らかです。それならばレースにおいて予測値のベストN頭について的中率と回収率を比較するのが素直なアプローチといえるでしょう。分類問題では予測ラベルではなく所属確率(1着の所属確率など)を予測値としてベストN頭を選出し、そのN頭についての各馬券種のN頭BOXの的中率、回収率、回収率の標準偏差を算出します。回収率の標準偏差は、たまたま大きな当たりを当てたのか平均的に高い回収率を安定して出しているのかを判断する材料となります。
また、評価値がどれくらいからが良い値なのかがモデル性能評価単体ではわかりにくいのでベースラインを用意します。ベースラインには確定単勝オッズ(人気)のトップN頭について同様の評価をおこないます。オッズは日本全国の馬券購入者の集合知であり、非常に手強い相手となるでしょう。
モデル評価の実践
では、試しに実際のデータを使って学習した3種類のモデルを評価してみます。
対象のレース条件は今週末に開催される弥生賞(GII)に合わせて中山芝2000mとしました。訓練データを2014年1月2015年12月(181レース)、評価用のテストデータを2016年1月2016年12月(50レース)とします。
予測モデルの入力となる特徴量は前回の記事で使用したものと同じ特徴量を使います。試したモデルは以下の通りです。
| モデル | 分類・回帰 | 目的変数 |
|---|---|---|
| k-NN | 二値分類 | 1着フラグ(1着ならばTrue, それ以外はFalse) |
| k-NN | 二値分類 | 複勝フラグ(複勝圏内ならばTrue, それ以外はFalse) |
| 線形モデル | 回帰 | 走破タイム(秒に変換) |
k-NNについては第6回理論記事で簡単な説明をしているのでそちらをご参照下さい。パラメータはscikit-learnのデフォルト値をそのまま使用し、不均衡データもそのままのナイーブな設定の下でモデルの比較をします。
各テストレースにおける予測値ベスト1~3までの的中率、回収率、回収率の標準偏差を以下に示します。表の見方は、行のwin、place、quinella place、quinella、 exacta、 trio, trifectaがそれぞれ単勝、複勝、ワイド、馬連、馬単、3連復、3連単、列のhit, ret, std_retが的中率、回収率、回収率の標準偏差を表しています。
- 1着・二値分類 (k-NN)
---- Top-1
hit ret std_ret
win 0.209 0.598 1.243
place 0.395 0.702 1.054
---- Top-2
hit ret ret_std
win 0.349 0.785 1.875
place 0.605 0.735 0.878
quinella place 0.116 0.891 2.718
quinella 0.070 1.205 5.273
exacta 0.070 0.876 3.738
---- Top-3
hit ret ret_std
win 0.535 0.764 1.283
place 0.721 0.701 0.665
quinella place 0.372 0.871 1.521
quinella 0.163 1.082 3.584
exacta 0.163 1.123 4.224
trio 0.000 0.000 0.000
trifecta 0.000 0.000 0.000
- 複勝圏内・二値分類(k-NN)
---- Top-1
hit ret ret_std
win 0.209 0.995 3.239
place 0.419 0.788 1.194
---- Top-2
hit ret ret_std
win 0.372 0.937 2.064
place 0.651 0.856 0.879
quinella place 0.279 1.600 3.333
quinella 0.070 2.019 8.983
exacta 0.070 1.926 9.596
---- Top-3
hit ret ret_std
win 0.512 0.829 1.389
place 0.767 0.971 1.234
quinella place 0.442 1.178 1.984
quinella 0.209 1.378 3.554
exacta 0.209 1.325 3.660
trio 0.093 2.114 8.917
trifecta 0.093 1.902 8.041
- 走破タイム・回帰(線形モデル)
---- Top-1
hit ret ret_std
win 0.186 0.579 1.362
place 0.326 0.505 0.788
---- Top-2
hit ret ret_std
win 0.395 0.733 1.469
place 0.628 0.619 0.606
quinella place 0.163 0.442 1.165
quinella 0.140 1.044 3.212
exacta 0.140 0.951 3.002
---- Top-3
hit ret ret_std
win 0.512 0.637 1.009
place 0.744 0.705 0.549
quinella place 0.419 0.662 0.950
quinella 0.233 0.724 1.812
exacta 0.233 0.588 1.381
trio 0.047 0.198 1.029
trifecta 0.047 0.131 0.666
- 確定単勝オッズ(ベースライン)
---- Top-1
hit ret ret_std
win 0.42 0.924 1.233
place 0.72 0.918 0.601
---- Top-2
hit ret ret_std
win 0.62 0.880 0.861
place 0.90 0.847 0.421
quinella place 0.32 0.788 1.365
quinella 0.18 0.788 1.834
exacta 0.18 0.773 1.952
---- Top-3
hit ret ret_std
win 0.74 0.819 0.694
place 0.96 0.881 0.370
quinella place 0.66 0.927 0.957
quinella 0.44 1.024 1.385
exacta 0.44 0.942 1.328
trio 0.10 0.786 2.748
trifecta 0.10 0.482 1.850
二値分類問題の1着二値分類と複勝二値分類を比較すると単勝的中性能は1着二値分類、複勝的中性能は複勝二値分類が高いことがわかります。学習している目的変数の意味を考えれば予想通りの結果といえるでしょう。また、複勝二値分類の回収率が高く良い予測ができているということも読み取れます。ワイド(quinella place)の上位3頭boxで的中率44.2%で回収率117%という攻守が安定した買い方もできそうです。走破タイム回帰は的中は二値分類と同等ながら回収率が低く、当てたとしても人気の馬を取れているだけのようなので、あまり価値のあるモデルとはいえないでしょう。
一方でベースラインを見てみると、的中性能はずば抜けており、いかに手強いかがよくわかります。しかし、回収率と合わせてみると複勝二値分類はだいたい勝っており、多くの人間が気がつかない穴馬をとる性能に優れているということが読み取れます。的中率でも確定単勝オッズの性能を越えようとするならば大量の有益な特徴量の追加、緻密なハイパーパラメータのチューニングなど数々の努力をしていく必要があります。
AlphaImpactでも開発当初は確定単勝オッズの壁の高さに苦労をしていましたが、現在はほぼ全ての条件において確定単勝オッズを越える的中性能を誇る予測モデルの生産をすることができるようになりました。
おわりに
一口に競馬予測といっても人それぞれ目指しているところが少しずつ異なると思います。圧倒的な的中率で単勝を当てたい、複勝量産マシーンをつくりたい、的中率は高くなくてもいいから人間では予想できないような大穴馬券を取りたいなど、どのような競馬人工知能が欲しいのかを予め定義しておかないと、モデルの評価軸がブレてしまい望んだモデルを手に入れることはできないでしょう。これから自分だけの競馬人工知能をつくる人は、是非自分がつくりたい競馬AIの性格を考えるところから始めてみてください。
次回からは機械学習で使われる代表的なモデルについて説明していきます。来週は線形モデルです。お楽しみに。
-
入力と出力に対する評価(報酬)の組からなる訓練データが与えられる状況で、政策関数と呼ばれる行動を選択する関数を学習する強化学習の3つに分類することもあります。 ↩︎