第5回 競馬予測の入力となる特徴量を作る

第5回の理論記事では機械学習アルゴリズムの入力となる特徴量の作り方について説明していきます。

特徴量とは？

競馬を機械学習アルゴリズムで解く場合、入力となるデータは下図のような行列として表されます。

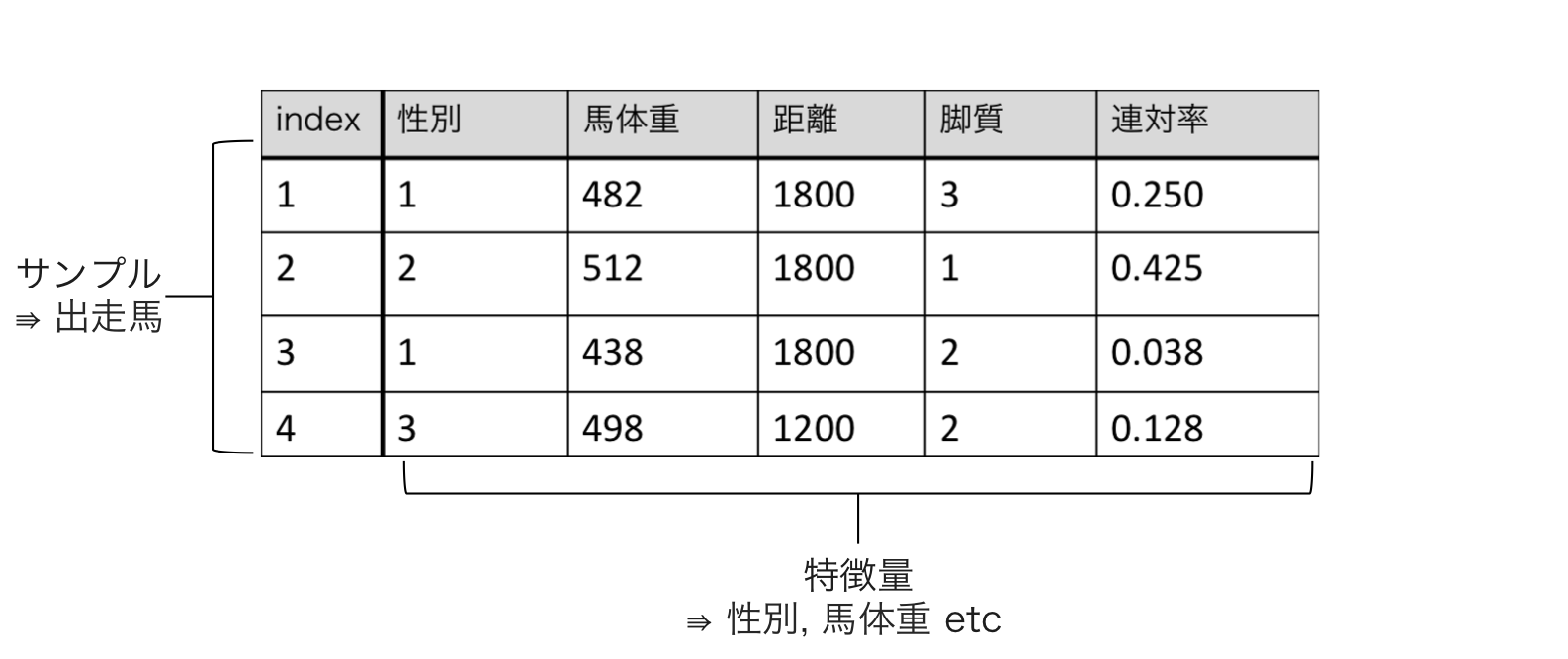
行列の各行はデータのサンプルで、1出走馬に対応します。各列は性別や距離など、その出走馬や出走レースの特性を定量化した値に対応しており、それを特徴量と呼びます。特徴量はデータのアイデンティティを決定づける量であり、たとえ異なる馬だとしても特徴量が一致している馬同士はどれだけ優れた機械学習アルゴリズムでも区別することはできません。また闇雲に無意味な特徴量を追加しても無価値なデータしか得られません。この原則は一般に**Garbage in, garbage out（ゴミを入れると、ゴミが出て来る）**と呼ばれています。したがって、精度が上がらなく悩んでいるときは、最新の論文の機械学習アルゴリズムを実装する前に、入力しているデータはゴミではないのかを良く見直す必要があります。

カテゴリデータを処理する

特徴量にはその数値の大きさそのものに意味のある数値データと数値がラベルとして意味しかもたないカテゴリデータがあります。さらにカテゴリデータには性別や競馬場コードなど識別子として使われる名義 (nominal) 特徴量と着順や脚質など順序付けが可能な順序 (ordinal) 特徴量に分けられます。

カテゴリデータをアルゴリズムの入力とするためには適切な処理を施す必要があります。

名義特徴量

上図の例では、名義特徴量である性別が数値（牡=1, 牝=2, 騙=3）として入っていますが、この数値の大小関係には意味がありません。そのため、名義特徴量は典型的な方法としてダミー変数に変換して特徴ベクトルとします。

ダミー変数とは1つの名義に対して0/1の2値ベクトルを割り当てた変数です。例えば性別のカテゴリデータは以下のようにダミー変数に変換できます。

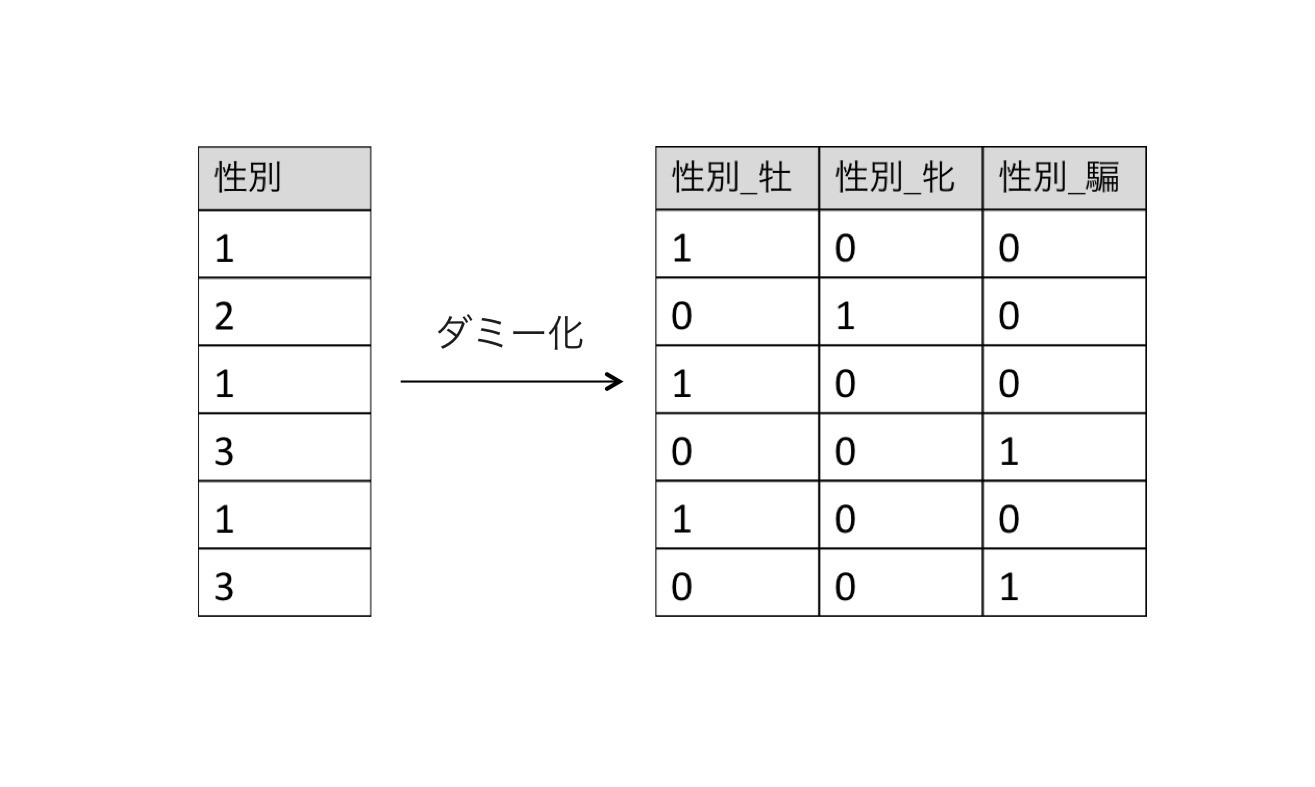
この変換はPandasのget_dummies()で1行で書くことができます。

>>> # x = [1, 2, 1, 3, 1, 3]
>>> pandas.get_dummies(x)
	1	2	3
0	1.0	0.0	0.0
1	0.0	1.0	0.0
2	1.0	0.0	0.0
3	0.0	0.0	1.0
4	1.0	0.0	0.0
5	0.0	0.0	1.0

このようにダミー変数に変換することで、0=該当カテゴリではない、1=該当カテゴリであるという意味を持たせることができます。ただ注意をしたいのが、カテゴリの数だけダミー変数の次元数が増加してしまうということです。性別は3種類なので問題はないですが、例えば競馬場は中央に10あるので10次元、騎手は約150人いるので150次元となります。

その次元を削減する方法としては、最も単純なものだと頻出上位のカテゴリだけを残す方法があります。もう少し理論的なアプローチだと、クラスタリングをして得られたラベルをカテゴリとする方法や決定木系アルゴリズムで特徴量の重要度を計算してフィルタリングする方法などがあります。ここの理論の詳細は今後の記事で紹介していきます。

順序特徴量

順序特徴量は着順や脚質など順序関係が定義できるカテゴリ変数です。名義特徴量と違いこちらは比較的扱いが簡単で、例えば脚質の場合は[逃げ, 先行, 差し, 追込] = [1, 2, 3, 4]のように定義すればそのまま特徴量として使うことができます。ただし脚質の場合は『逃げたかどうか』など単純な順序では測れない情報も含んでいるので、名義特徴量として扱うことも検討できます。

最後に

今回はカテゴリデータを主とした特徴量の作成方法について解説しましたが、その重要性を感じていただけたでしょうか。

すでに第5回目だというのにまだ予測ロジックについての話が出てこないではないかと思われてる方も多いかと思いますが、入力となるデータ作りはただの手の運動ではなく入念な設計が必要となるクリエイティブなプロセスで、実際のAlphaImpactの開発では予測ロジックの作成以上に時間を要しています¹。最強の競馬人工知能を作る一番の近道は最強の競馬特徴量職人になることだと言っても過言ではないでしょう。

次回の理論記事ではデータの前処理について説明していく予定です。